题目内容
16.目前“校园手机”现象越来越受到社会关注,针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“中学生带手机的”的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题: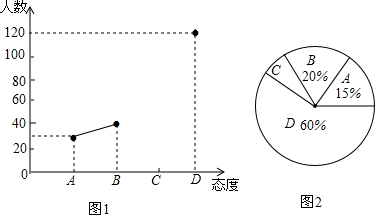
(1)此次抽样调查中,共调查了多少名名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对中学生带手机持反对态度,初三(2)班有B1、B2两位学生家长对中学生带手机也持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
分析 (1)用D类的人数除以它所占的百分比即可得到调查的总人数;
(2)用360°乘以C类所占的百分比得到扇形C所对的圆心角的度数,再用200乘以C类所占的百分比得到C类人数,然后补全图1;
(3)画树状图展示所有12种等可能结果,再找出2人来自不同班级的结果数,然后根据概率公式求解.
解答 解:(1)120÷60%=200(人),
所以调查的家长数为200人;
(2)扇形C所对的圆心角的度数=360°×(1-20%-15%-60%)=18°,
C类的家长数=200×(1-20%-15%-60%)=10(人),
补充图为: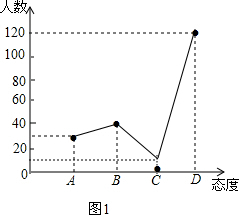
(3)设初三(1)班两名家长为A1、A2,初三(2)班两名家长为B1,B2,
画树状图为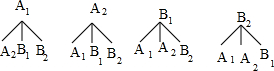
共有12种等可能结果,其中2人来自不同班级共有8种,
所以2人来自不同班级的概率=$\frac{8}{12}$=$\frac{2}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了扇形统计图.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
6.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
7.不等式2x+4≤0的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
4.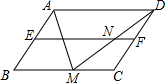 如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
 如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )| A. | 0.5 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
11.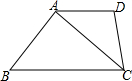 如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
 如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )
如图,四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=6,AD=4,则该四边形的面积为( )| A. | 9$\sqrt{7}$ | B. | 12 | C. | 8 | D. | 8$\sqrt{3}$ |
1.一块正方形的瓷砖,面积为$\sqrt{60}$cm2,它的边长大约在( )
| A. | 4cm~5cm之间 | B. | 5cm~6cm之间 | C. | 6cm~7cm之间 | D. | 7cm~8cm之间 |
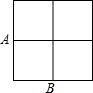 如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.
如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.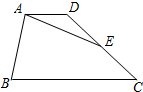 如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).
如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).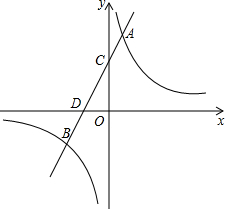 如图,直线y=mx+4与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.
如图,直线y=mx+4与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.