题目内容
6.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
分析 (1)计算出其平均值即可;
(2)概率接近于(1)得到的频率;
(3)首先确定40个球的颜色,然后使得黑球和白球的数量相等即可确定答案.
解答 解:(1)∵摸到白球的频率为(0.65+0.62+0.593+0.604+0.601+0.599+0.601)÷7≈0.6,
∴当实验次数为10000次时,摸到白球的频率将会接近0.6.
(2)∵摸到白球的频率为0.6,
∴假如你摸一次,你摸到白球的概率P(白球)=0.6.
(3)先得到盒子内白球数24,黑球数16;
增加8个黑球(或减少8个白球等).
点评 本题考查了用频率估计概率的知识,解题的关键是能够了解大量重复试验中,事件发生的频率约等于概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列命题中,真命题是( )
| A. | 两个无理数相加的和一定是无理数 | B. | 三角形的三条中线一定交于一点 | ||
| C. | 菱形的对角线一定相等 | D. | 同圆中相等的弦所对的弧一定相等 |
14.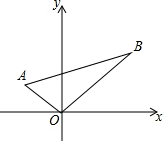 如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
 如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | ($\sqrt{3}$,$\sqrt{3}$) | D. | (2,2) |
18.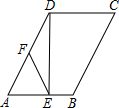 如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )
如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )
 如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )
如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 如图,延长?ABCD的边AB到点E,使BE=BC,延长CD到点F,使DF=DA,连结AF,CE,求证:四边形AECF是平行四边形.
如图,延长?ABCD的边AB到点E,使BE=BC,延长CD到点F,使DF=DA,连结AF,CE,求证:四边形AECF是平行四边形.