题目内容
20.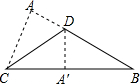 如图,将一张△ABC的纸片沿CD进行折叠,点A的对应点A′恰好落在BC上,CA′:A′B=3:2.若△ABC的面积为96,则△ACD的面积为( )
如图,将一张△ABC的纸片沿CD进行折叠,点A的对应点A′恰好落在BC上,CA′:A′B=3:2.若△ABC的面积为96,则△ACD的面积为( )| A. | 34 | B. | 30 | C. | 36 | D. | 56 |
分析 由CA′:A′B=3:2,根据等高三角形的面积比等于对应底的比,可求得S△A′CD:S△A′BD=3:2,又由折叠的性质可得S△A′CD=S△ACD,继而求得答案.
解答 解:∵CA′:A′B=3:2,
∴S△A′CD:S△A′BD=3:2,
由折叠的性质可得:△ACD≌△A′CD,
即S△A′CD=S△ACD,
∴S△ACD=$\frac{3}{8}$S△ABC=$\frac{3}{8}$×96=36.
故选C.
点评 此题考查了折叠的性质.注意掌握等高三角形面积的比等于其对应底的比是关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
11.某公司为迎接2014年的巴西世界杯,特制作如图所示1的电子广告牌,并且该广告牌10秒后字样会进行一次上下调换如图2,再过10秒字样又进行一次左右调换(如图3),之后再进行上下调换,…,以此循环,广告牌上的字样要和最初相同,至少需经过( )
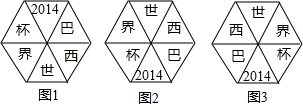

| A. | 30秒 | B. | 40秒 | C. | 50秒 | D. | 60秒 |
15.下列说法中,不正确的是( )
| A. | 为了了解一批汽车轮胎的使用年限,应采用抽样调查的方式 | |
| B. | “50名同学中恰有2名同学的生日是同一天”属于随机事件 | |
| C. | “早晨的太阳从东方升起”属于必然事件 | |
| D. | “长为3cm,5cm,9cm的三条线段围成一个三角形”属于可能事件 |
5.下列说法中,正确的是( )
| A. | 如果a2=b2,那么a=b | B. | 如果ac=bc,那么a=b | ||
| C. | 如果a=b,那么2a+c=b+2c | D. | 如果a-c=b-c,那么a=b |
12.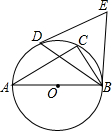 如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )
如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )
 如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )
如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 等边三角形 | D. | 无法确定 |
10. 如图,直线a、b被直线c、d所截,若∠1=∠2,∠3=115°,则∠4的度数为( )
如图,直线a、b被直线c、d所截,若∠1=∠2,∠3=115°,则∠4的度数为( )
 如图,直线a、b被直线c、d所截,若∠1=∠2,∠3=115°,则∠4的度数为( )
如图,直线a、b被直线c、d所截,若∠1=∠2,∠3=115°,则∠4的度数为( )| A. | 55° | B. | 60° | C. | 65° | D. | 75° |
 小明在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图均为如图,则构成该几何体的小立方块的个数可能是( )
小明在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图均为如图,则构成该几何体的小立方块的个数可能是( )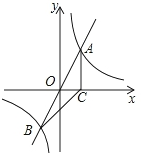 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.