题目内容
12.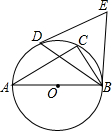 如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )
如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 等边三角形 | D. | 无法确定 |
分析 根据切线的性质得出DE=BE,利用圆周角定理得出∠DBE=60°,进而判断三角形的形状.
解答 解:∵分别过点B、D作⊙O的切线,
∴DE=BE,
∵D是劣弧AC的中点,
∴∠DBA=∠DBC,
∵∠A=30°,AB是⊙O的直径,
∴∠ABD=30°,
∵过点B、D作⊙O的切线,
∴∠ABE=90°,
∴∠DBE=60°,
△BDE的形状是等边三角形,
故选C
点评 本题考查了切线的性质,关键是根据切线的性质得出DE=BE.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
7. 如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )
如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )
 如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )
如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )| A. | 互相平行 | B. | 互相垂直 | C. | 不相交也不平行 | D. | 无法确定 |
4.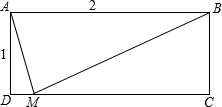 矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
 矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{4}$ | C. | $\sqrt{3}-\frac{3}{2}$ | D. | $2-\sqrt{3}$ |
1.可以用来说明命题“若m<n,则$\frac{1}{m}$$>\frac{1}{n}$”是假命题的反例是( )
| A. | m=2,n=-3 | B. | m=-2,n=3 | C. | m=-2,n=-3 | D. | m=2,n=3 |
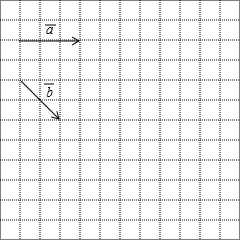 如图,在正方形网格中,每一个小正方形的边长都是1,已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点,如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模(不用写作法,只要所求作向量).
如图,在正方形网格中,每一个小正方形的边长都是1,已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点,如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模(不用写作法,只要所求作向量).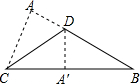 如图,将一张△ABC的纸片沿CD进行折叠,点A的对应点A′恰好落在BC上,CA′:A′B=3:2.若△ABC的面积为96,则△ACD的面积为( )
如图,将一张△ABC的纸片沿CD进行折叠,点A的对应点A′恰好落在BC上,CA′:A′B=3:2.若△ABC的面积为96,则△ACD的面积为( ) 高铁和特快两列火车分别从相距1000千米路程的甲、乙两地同时出发,先相向而行,高铁到达乙地后,停留1小时,然后按原路原速返回,高铁比特快晚1小时到达甲地,高铁和特快两列火车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示,假定这两列火车均匀速行驶.
高铁和特快两列火车分别从相距1000千米路程的甲、乙两地同时出发,先相向而行,高铁到达乙地后,停留1小时,然后按原路原速返回,高铁比特快晚1小时到达甲地,高铁和特快两列火车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示,假定这两列火车均匀速行驶.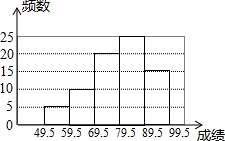 某校八年级(2)班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全部人数的( )
某校八年级(2)班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全部人数的( )