题目内容
10.等腰三角形腰长为2cm,底边长为2$\sqrt{3}$cm,则顶角为120°,面积为$\sqrt{3}$cm2..分析 作底边上的高,根据等腰三线合一的性质,也是底边上的中线,利用勾股定理求出底边上的高,然后代入面积公式求解即可.
解答 解:如图,作AD⊥BC于D,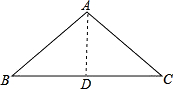
∴BD=DC=$\sqrt{3}$cm,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{{2}^{2}-(\sqrt{3})^{2}}=1$cm,
∴∠B=30°,
∴顶角为180°-30°-30°=120°,三角形的面积=$\frac{1}{2}$×2$\sqrt{3}$×1=$\sqrt{3}$cm2.
故答案为:120°;$\sqrt{3}$cm2.
点评 本题考查解直角三角形问题,关键是利用等腰三角形三线合一和勾股定理求解.

练习册系列答案
相关题目
3.将235000000用科学记数法表示为( )
| A. | 235×106 | B. | 2.35×107 | C. | 2.35×108 | D. | 2.35×109 |
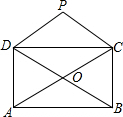 如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD.
如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD.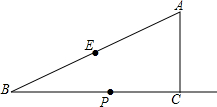 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为2或2$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为2或2$\sqrt{3}$.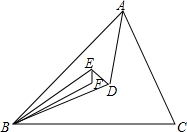 如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.
如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.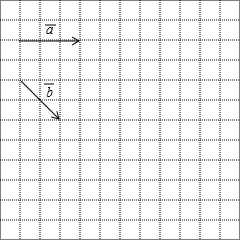 如图,在正方形网格中,每一个小正方形的边长都是1,已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点,如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模(不用写作法,只要所求作向量).
如图,在正方形网格中,每一个小正方形的边长都是1,已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点,如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模(不用写作法,只要所求作向量).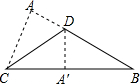 如图,将一张△ABC的纸片沿CD进行折叠,点A的对应点A′恰好落在BC上,CA′:A′B=3:2.若△ABC的面积为96,则△ACD的面积为( )
如图,将一张△ABC的纸片沿CD进行折叠,点A的对应点A′恰好落在BC上,CA′:A′B=3:2.若△ABC的面积为96,则△ACD的面积为( )