题目内容
18.如图,在平行四边形ABCD中,∠D=90°,边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根.点P从点A出发,以每秒1个单位的速度,沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).(1)求AB与BC的长;
(2)在点P的运动过程中,是否存在点P,使△CDP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.
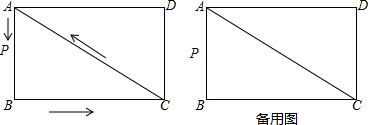
分析 (1)解方程x2-7x+12=0,即可求出AB与BC的长;
(2)存在点P,使△CDP是等腰三角形,利用已知条件易证四边形ABCD是矩形,利用勾股定理可求出AC的长,再分别讨论P在不同位置下时△CDP为等腰三角形,求出t的值即可.
解答 解:(1)∵x2-7x+12=(x-3)(x-4)=0,
∴x=3或4,
∵边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根,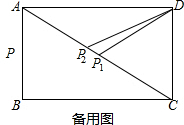
∴AB=3,BC=4;
(2)存在点P,使△CDP是等腰三角形,
理由如下:
∵在平行四边形ABCD中,∠D=90°,
∴四边形ABCD是矩形,
当P1D=P1C即P为对角线AC中点时,△CDP是等腰三角形,
∵AB=3,BC=4,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴CP1=$\frac{1}{2}$AC=2.5,
∴t=$\frac{3+4+2.5}{1}$=9.5(秒);
当P2D=P2C时,△CDP是等腰三角形,
∴t=$\frac{3+4+3}{1}$=10(秒),
AB的中点也是,此时t=1;
CP=CD,P在BC线段上,此时,t=4;
DP=DC,P在斜边AC上,此时t=10.6;
综上可知当t=9.5秒或10秒或1秒或4秒或10.6秒时△CDP是等腰三角形
点评 本题考查了平行四边形的性质、矩形的判定和性质,等腰三角形的判定和性质性质以及勾股定理的运用,解题的关键是利用分类讨论的思想解答题目,做到不重不漏.

练习册系列答案
相关题目
6.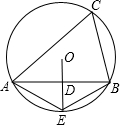 如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论:①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤弧AE=弧BE,正确结论的个数是( )
如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论:①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤弧AE=弧BE,正确结论的个数是( )
 如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论:①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤弧AE=弧BE,正确结论的个数是( )
如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论:①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤弧AE=弧BE,正确结论的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.若二次函数y=ax2+$\sqrt{2}$(a≠0),当x分别取x1,x2时,函数值相等,则当x取x1+x2时,函数值为( )
| A. | 0 | B. | a | C. | $\sqrt{2}$ | D. | 不确定 |
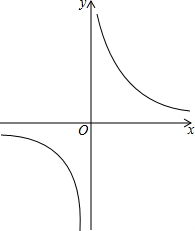 反比例函数y=$\frac{k-1}{x}$如图,则:
反比例函数y=$\frac{k-1}{x}$如图,则: 如图,钝角三角形ABC的面积为18,最长边AB=12,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为3.
如图,钝角三角形ABC的面积为18,最长边AB=12,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为3.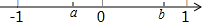 实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.