题目内容
3. 如图,钝角三角形ABC的面积为18,最长边AB=12,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为3.
如图,钝角三角形ABC的面积为18,最长边AB=12,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为3.
分析 过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,则CE即为CM+MN的最小值,再根据三角形的面积公式求出CE的长,即为CM+MN的最小值.
解答 解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,
∵BD平分∠ABC,ME⊥AB于点E,MN⊥BC于N
∴MN=ME,
∴CE=CM+ME=CM+MN的最小值.
∵三角形ABC的面积为18,AB=12,
∴$\frac{1}{2}$×12•CE=18,
∴CE=3.
即CM+MN的最小值为3.
故答案为:3.
点评 本题考查了轴对称-最短路线问题,关键是画出符合条件的图形,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目
13.在直角坐标系中,O为坐标原点,已知A(2,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 如图,分别以△ABC的边AB、AC为直角边向外作等腰Rt△ABD、Rt△ACE.连结BE、CD,且交于点Q,求证:OA平分∠DOE.
如图,分别以△ABC的边AB、AC为直角边向外作等腰Rt△ABD、Rt△ACE.连结BE、CD,且交于点Q,求证:OA平分∠DOE.
 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,则∠AEB=36°.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,则∠AEB=36°. 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=4,则CD的长为8.
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=4,则CD的长为8.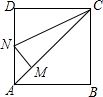 如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°.
如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°.