题目内容
7.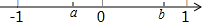 实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
分析 根据数轴得到a、b、a-b的符号,然后去根号.
解答 解:如图所示,a<0<b,且|a|<|b|,
∴$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$=|a|•|b|+|a-b|=-ab+b-a.
故答案是:-ab+b-a.
点评 本题考查了二次根式的性质与化简,实数与数轴.解题的关键是根据数轴得到a、b的取值范围.

练习册系列答案
相关题目
 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=4,则CD的长为8.
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=4,则CD的长为8. 如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2,则平行四边形ABCD的周长为4$\sqrt{2}$.
如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2,则平行四边形ABCD的周长为4$\sqrt{2}$.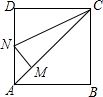 如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°.
如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°. 如图,∠1=130°,∠2=130°,∠3=120°,试确定∠4的度数.
如图,∠1=130°,∠2=130°,∠3=120°,试确定∠4的度数. 如图,直角梯形ABCD的中位线EF=4,垂直于底的腰AB=5,则图中阴影部分的面积是10.
如图,直角梯形ABCD的中位线EF=4,垂直于底的腰AB=5,则图中阴影部分的面积是10.