题目内容
13.已知方程组$\left\{\begin{array}{l}{5x+y=3}\\{mx+5y=4}\end{array}\right.$与$\left\{\begin{array}{l}{x-2y=5}\\{5x+ny=1}\end{array}\right.$有相同的解,则m-n=12.分析 首先解方程组$\left\{\begin{array}{l}{5x+y=3}\\{x-2y=5}\end{array}\right.$,即可求得方程组的解,然后把方程组的解代入含有m,n的两个方程,即可求解出m,n的值,即可解答.
解答 解:方程组$\left\{\begin{array}{l}{5x+y=3}\\{x-2y=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$代入方程mx+5y=4得:m-10=4,
解得:m=14,
把$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$代入方程5x+ny=1得:5-2n=1,
解得:n=2,
则m-n=14-2=12,
故答案为:12.
点评 本题主要考查了方程组的解的定义,首先求得方程组的解是解题的关键.

练习册系列答案
相关题目
3.某地2010年投入教育经费2100万元,预计2012年投入3500元.设这两年投入教育经费的年平均增长率为x,则下列方程正确的是( )
| A. | 2100x2=3500 | B. | 2100(1+x)2=3500 | ||
| C. | 2100(1+x%)2=3500 | D. | 2100(1+x)+2100(1+x)2=3500 |
 如图,在?ABCD中,E、F分别为边AB、CD的中点,AG∥DB交CB的延长线于点G.
如图,在?ABCD中,E、F分别为边AB、CD的中点,AG∥DB交CB的延长线于点G.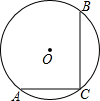 如图,在⊙O中,弦AC⊥BC,若AC=6cm,BC=8cm,则⊙O的半径为5cm.
如图,在⊙O中,弦AC⊥BC,若AC=6cm,BC=8cm,则⊙O的半径为5cm.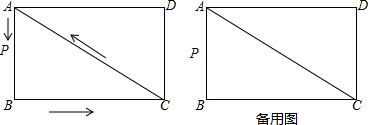
 如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2,则平行四边形ABCD的周长为4$\sqrt{2}$.
如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2,则平行四边形ABCD的周长为4$\sqrt{2}$.