题目内容
11.在等边△ABC中,点E在AB上,点D在CB延长线上,且ED=EC.(1)当点E为AB中点时,如图①,AE=DB(填“>”“<”或“=”)
(2)当点E为AB上任意一点时,如图②,AE=DB(填“>”“<”或“=”),并说明理由.(提示:过E作EF∥BC,交AC于点F)

分析 (1)先证AE=BE,再证∠D=∠DEB,得出DB=BE,即可得出DB=AE;
(2)过点E作EF∥BC,交AC于F,先证明△AEF是等边三角形,得出AE=EF,再证明△DBE≌△EFC,得出DB=EF,即可证出AE=DB.
解答 解:(1)∵△ABC是等边三角形,E为AB的中点,
∴∠ABC=60°,AE=BE,∠ECB=30°,
∵ED=EC,
∴∠D=∠ECB=30°,
∵∠ABC=∠D+∠DEB,
∴∠DEB=30°,
∴∠D=∠DEB,
∴DB=BE,
∴DB=AE;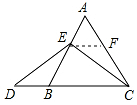
故答案为:=;
(2)DB=AE成立;理由如下:
过点E作EF∥BC,交AC于F,如图2所示:则∠AEF=∠ABC,∠AFE=∠ACB,∠CEF=∠ECD,
∵∠A=∠ABC=∠ACB=60°,
∴∠A=∠AEF=∠AFE=60°,
∠DBE=120°,
∴△AEF是等边三角形,∴AE=EF,∠EFC=120°,
∴BE=CF,∠DBE=∠EFC,
∵ED=EC,
∴∠D=∠ECD,
∴∠D=∠CEF,
在△DBE和△EFC中,$\left\{\begin{array}{l}{∠D=∠CEF}&{\;}\\{∠DBE=∠EFC}&{\;}\\{BE=CF}&{\;}\end{array}\right.$,
∴△DBE≌△EFC(AAS),
∴DB=EF,
∴AE=DB;
故答案为:=.
点评 本题考查了等边三角形的性质与判定、等腰三角形的性质、全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.为确保信息安全,信息需加密传输,发送方由明文→密文(加密);接收方由密文→明文(解密).已知加密规则为:明文a,b,c对应密文a+2b,2b+c,3c.例如:明文1,2,3对应的密文5,7,9.当接收方收到密文14,9,15时,则解密得到的明文为( )
| A. | 10,5,2 | B. | 10,2,5 | C. | 2,5,10 | D. | 5,10,2 |
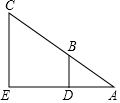 如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=12m,则河宽DE=6m.
如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=12m,则河宽DE=6m. 如图,AC与BD交于O点,AB∥DC,AB=DC.
如图,AC与BD交于O点,AB∥DC,AB=DC.