题目内容
19.用适当的方法解方程:x2-6x+9=(5-2x)2.分析 先把x2-6x+9=(5-2x)2转化为(x-3)2-(5-2x)2=0,然后因式分解得到(-x+2)(3x-8)=0,解两个一元一次方程即可.
解答 解:∵x2-6x+9=(5-2x)2,
∴(x-3)2=(5-2x)2,
∴(x-3)2-(5-2x)2=0,
∴[(x-3)+(5-2x)][(x-3)-(5-2x)]=0,
∴(x-3+5-2x)(x-3-5+2x)=0,
∴(-x+2)(3x-8)=0,
∴-x+2=0或3x-8=0,
∴x1=2,x2=$\frac{8}{3}$.
点评 本题主要考查了因式分解法解一元二次方程的知识,解答本题的关键是熟练掌握解因式分解法解一元二次方程的基本步骤,此题难度不大.

练习册系列答案
相关题目
9.分解因式后结果是-3(x-y)2的多项式是( )
| A. | -3x2+6xy-3y2 | B. | 3x2-6xy-y2 | C. | 3x2-6xy+3y2 | D. | -3x2-6xy-3y2 |
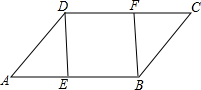 如图所示,已知AB=CD,AD=BC,DE=BF,且E,F分别是AB,CD的中点.
如图所示,已知AB=CD,AD=BC,DE=BF,且E,F分别是AB,CD的中点.
 如图,在Rt△AOB中,∠AOB=90°,OA=OB=4,点C、D在边AB上,且∠COD=45°,设AD=x,BC=y.
如图,在Rt△AOB中,∠AOB=90°,OA=OB=4,点C、D在边AB上,且∠COD=45°,设AD=x,BC=y.