题目内容
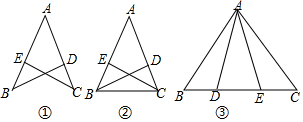
16. 如图,AC与BD交于O点,AB∥DC,AB=DC.
如图,AC与BD交于O点,AB∥DC,AB=DC.(1)点O是AC、BD的中点吗?说明你的理由;
(2)若过O点作直线l,分别交AB、DC于E、F两点,OE=OF吗?说明你的理由.
分析 (1)由AB∥DC,根据平行线的性质,可得∠A=∠C,∠B=∠D,又由AB=DC,即可利用ASA判定△AOB≌△COD,继而证得结论;
(2)由(1),可直接利用ASA判定△AOE≌△COF,继而证得OE=OF.
解答 解:(1)点O是AC、BD的中点;理由如下:
∵AB∥DC,
∴∠A=∠C,∠B=∠D,
在△AOB和△COD中,$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{AB=CD}&{\;}\\{∠B=∠D}&{\;}\end{array}\right.$,
∴△AOB≌△COD(ASA),
∴OA=OC,OB=OD,
即点O是AC、BD的中点;
(2)OE=OF;理由如下:
在△AOE和△COF中,$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{OA=OC}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF,
∴OE=OF.
点评 此题考查了全等三角形的判定与性质以及平行线的性质.注意利用平行线的性质,证得三角形全等是解此题的关键.

练习册系列答案
相关题目
6.要把面值为10元一张的人民币换成零饯现有足够的面值为2元、1元的人民币,则有几种换法( )
| A. | 5种 | B. | 6种 | C. | 8种 | D. | 10种 |

 如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠EDB.求证:∠3=∠4.
如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠EDB.求证:∠3=∠4. 某数学兴趣小组为了估计河的宽度,在河对岸选定一个8标点P,在近岸取点Q和S,使点P,Q,S共线且直找PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QS=60m,请计算河的宽度PQ.
某数学兴趣小组为了估计河的宽度,在河对岸选定一个8标点P,在近岸取点Q和S,使点P,Q,S共线且直找PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QS=60m,请计算河的宽度PQ. 在平面直角坐标系中,点A(0,4$\sqrt{3}$),B(m,-2$\sqrt{3}$),C(n,-2$\sqrt{3}$),且m,n满足$\sqrt{m+3n}$+(n-6)2=0,线段BC交y轴于点H.
在平面直角坐标系中,点A(0,4$\sqrt{3}$),B(m,-2$\sqrt{3}$),C(n,-2$\sqrt{3}$),且m,n满足$\sqrt{m+3n}$+(n-6)2=0,线段BC交y轴于点H.