题目内容
6．
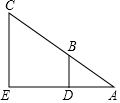如图，小东设计两个直角，来测量河宽DE，他量得AD=2m，BD=3m，CE=12m，则河宽DE=6m．
分析 由于BD∥CE，所以△ABD∽△ACE，利用对应边的比相等即可求出ED的长度．
解答 解：∵BD∥CE，
∴△ABD∽△ACE，
∴$\frac{BD}{CE}=\frac{AD}{AE}$，
∴$\frac{3}{12}=\frac{2}{AE}$，
∴AE=8，
∴ED=AE-AD=6m，
故答案为：6
点评 本题考查相似三角形的应用，属于基础题型．
练习册系列答案
相关题目
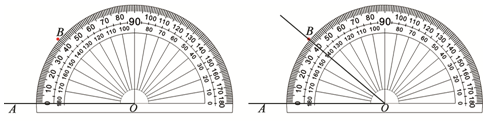
5．如图，在利用量角器画一个40°的∠AOB的过程中，对于先找点B，再画射线OB这一步骤的画图依据，喜羊羊同学认为是两点确定一条直线，懒羊羊同学认为是两点之间线段最短．你认为喜羊羊同学的说法是正确的．
将一个正方形纸片剪成如图中的四个小正方形，用同样的方法，每个小正方形又被剪成四个更小的正方形，这样连续5次后共得到16个小正方形．
如图，在Rt△AOB中，∠AOB=90°，OA=OB=4，点C、D在边AB上，且∠COD=45°，设AD=x，BC=y．
18．
连接边长为1的正方形对边中点，可将一个正方形分成四个全等的小正方形，选右下角的小正方形进行第二次操作，又可将这个小正方形分成四个更小的小正方形，…重复这样的操作，则2016次操作后右下角的小正方形面积是（ ）
连接边长为1的正方形对边中点，可将一个正方形分成四个全等的小正方形，选右下角的小正方形进行第二次操作，又可将这个小正方形分成四个更小的小正方形，…重复这样的操作，则2016次操作后右下角的小正方形面积是（ ）| A． | $\frac{1}{2004}$ | B． | ${（\frac{1}{2}）^{2016}}$ | C． | ${（\frac{1}{4}）^{2016}}$ | D． | $1-{（\frac{1}{4}）^{2016}}$ |
如图，四边形ABCD与ECGF是两个边长分别为a，b的正方形，写出a，b表示阴影部分面积的代数式，并计算当a=2，b=8时，阴影部分的面积．