题目内容
 如图,已知直线y=-
如图,已知直线y=-| 3 |
| 3 |
考点:圆的综合题
专题:代数几何综合题,数形结合
分析:先根据当AD与⊙C相切,且在x轴的上方时,△ABE的面积最小,连接CD,则CD⊥AD,再求出A、B两点的坐标,再根据勾股定理求出AD,从而得出S△ACD,再根据△AOE∽△ADC,求出△ABE的面积,再根据当AD与⊙C相切,且在x轴的下方时,△ABE的面积最大,求出△ABE的面积,即可得出△ABE面积S的取值范围.
解答: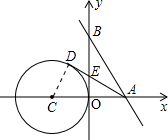 解:当AD与⊙C相切,且在x轴的上方时,△ABE的面积最小,
解:当AD与⊙C相切,且在x轴的上方时,△ABE的面积最小,
连接CD,则CD⊥AD,
∵直线y=-
x+2
与两坐标轴分别交于A、B两点,
∴A、B两点的坐标是(2,0),(0,2
),
在Rt△ACD中,CD=2,AC=OC+OA=4;
由勾股定理,得:AD=2
;
∴S△ACD=
AD•CD=
×2
×2=2
;
∵△AOE∽△ADC,
∴
=(
)2=(
)2=
,
∴S△AOE=
S△ADC=
;
∴S△ABE=S△AOB-S△AOE=
×2×2
-
=
;
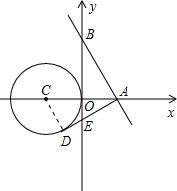
当AD与⊙C相切,且在x轴的下方时,△ABE的面积最大,
连接CD,则CD⊥AD,
则S△ABE=S△AOB+S△AOE=
×2×2
+
=
;
则△ABE面积S的取值范围是
≤S≤
.
故答案为:
≤S≤
.
 解:当AD与⊙C相切,且在x轴的上方时,△ABE的面积最小,
解:当AD与⊙C相切,且在x轴的上方时,△ABE的面积最小,连接CD,则CD⊥AD,
∵直线y=-
| 3 |
| 3 |
∴A、B两点的坐标是(2,0),(0,2
| 3 |
在Rt△ACD中,CD=2,AC=OC+OA=4;
由勾股定理,得:AD=2
| 3 |
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵△AOE∽△ADC,
∴
| S△AOE |
| S△ADC |
| AO |
| AD |
| 2 | ||
2
|
| 1 |
| 3 |

∴S△AOE=
| 1 |
| 3 |
2
| ||
| 3 |
∴S△ABE=S△AOB-S△AOE=
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
| 4 |
| 3 |
| 3 |
当AD与⊙C相切,且在x轴的下方时,△ABE的面积最大,
连接CD,则CD⊥AD,
则S△ABE=S△AOB+S△AOE=
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
| 8 |
| 3 |
| 3 |
则△ABE面积S的取值范围是
| 4 |
| 3 |
| 3 |
| 8 |
| 3 |
| 3 |
故答案为:
| 4 |
| 3 |
| 3 |
| 8 |
| 3 |
| 3 |
点评:此题考查了圆的综合,用到的知识点是切线的性质、勾股定理、相似三角形的性质,关键是根据题意画出图形,求出△ABE的面积的最大值和最小值.

练习册系列答案
相关题目
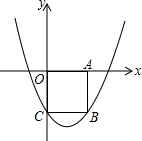 如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴正半轴、y轴的负半轴上,二次函数
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴正半轴、y轴的负半轴上,二次函数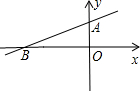 已知如图,直线
已知如图,直线 如图,△ABC的三边BC,AC,AB的长分别为3cm,4cm,5cm,把△ABC沿最长边AB翻转180°得△ABC′,连接CC′,求CC′的长.
如图,△ABC的三边BC,AC,AB的长分别为3cm,4cm,5cm,把△ABC沿最长边AB翻转180°得△ABC′,连接CC′,求CC′的长.