Question

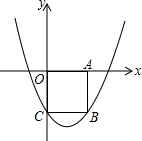如图，在平面直角坐标系xOy中，边长为2的正方形OABC的顶点A、C分别在x轴正半轴、y轴的负半轴上，二次函数y=

2

3

(x-h)2+k的图象经过B、C两点．
（1）求该二次函数的顶点坐标；
（2）结合函数的图象探索：当y＞0时x的取值范围；
（3）设m＜

1

2

，且A（m，y₁），B（m+1，y₂）两点都在该函数图象上，试比较y₁、y₂的大小，并简要说明理由．

Answer 1

考点：二次函数的性质,二次函数图象上点的坐标特征,二次函数与不等式（组）

专题：代数几何综合题,待定系数法

分析：（1）根据正方形的性质得出点B、C的坐标，根据二次函数的对称性得出h的数值，再进一步代入一点求出k的数值即可求出顶点坐标；
（2）由（1）函数解析式求出与x轴交点的坐标解决问题；
（3）根据二次函数的对称性与点A（m，y₁）对称的点为（2-m，y₁），根据图形，比较得出结论．

解答：解：（1）∵正方形OABC的边长为2，
∴点B、C的坐标分别为（2，-2），（0，-2），
对称轴x=h=

0+2

2

=1，
把C（0，-2）代入二次函数y=

2

3

(x-h)2+k，
解得k=-

8

3

，
∴二次函数的顶点坐标为（1，-

8

3

）；
（2）当y=0时，

2

3

（x-1）²-

8

3

=0，
解得x₁=-1，x₂=3，
∴当y＞0时x＜-1或x＞3；
（3）点A（m，y₁）关于x=1对称点为：（2-m，y₁），
∵m＜

1

2

，
∴m+1＜2-m＞
∴y₁＞y₂．

点评：此题考查二次函数的性质，待定系数法求函数解析式，二次函数的对称性以及利用图象解决问题．