Question

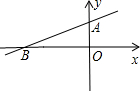已知如图，直线y=

3

3

x+2与坐标轴交于A、B两点，若点P是直线AB上的一个动点，试在坐标平面内找一点Q，使以O、B、P、Q为顶点的四边形为菱形，则Q的坐标是

 

．

Answer 1

考点：一次函数综合题

专题：代数几何综合题,分类讨论

分析：因为菱形的四个边相等，要使以点O、B、P、Q为顶点构成的四边形为菱形，根据OB为菱形的对角线，OB为菱形的边两种情况，分别求出符合条件的N点坐标．．

解答：解：令y=

3

3

x+2=0，
解得x=-2

3

，
∴点B的坐标为（-2

3

，0），
令x=0，y=2，
∴点A的坐标为（0，2），
①当OB为菱形的对角线时，如图1，由OB=2

3

可知，P点横坐标为-

3

，
代入直线y=

3

3

x+2中，得M点纵坐标为1，
∵M、N关于y轴对称，
∴Q（-

3

，-1）；

②当OB为菱形的边时，如图2，
作PM⊥交x轴于P点，
∵OB=2

3

，OA=2，
∴AB=

(2 3 )2+22

=4，
由△P₂MB∽△AOB，
得

OA

P2M

=

AB

P2B

=

OB

MB

，即

2

P2M

=

4

2 3

=

2 3

MB

得P₂M=

3

，MB=3，
∴Q₂坐标为（-3，-

3

）
同理可得Q₁（3，

3

），Q₃（-

3

，3），
故答案为：(-

3

，-1)或(3，

3

)或(-

3

，3)或(-3，-

3

)

点评：本题考查了一次函数的综合运用，一次函数图象上点的坐标特点，菱形的性质，关键是根据OB为菱形的对角线菱形的边，分类讨论求解．