题目内容
7．公路L一侧有A、B两工厂，欲在公路边合建一座仓库，请分别按下列要求找出所建仓库的位置（保留作图痕迹）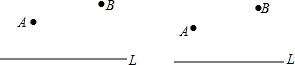
（1）两厂到仓库的距离相等；
（2）两厂到仓库的距离之和最短．
分析 （1）仓库到A、B的距离相等，仓库应在AB的垂直平分线上；
（2）距离之和最短，应作出A关于直线L的对称点A'，连接A'B，与L的交点即是所求的点．
解答 解：（1）如图1，作线段AB的垂直平分线，交直线L于P点，点P即为所求；
（2）如图2，作A关于直线L的对称点A′，连接AB，交直线L于P点，点P就是所求．
点评 本题用到的知识点为：到平面内两个点距离相等的点应在连接这两点的线段的垂直平分线上．求两点和距离最小应作出一点的轴对称图形．然后连接对称点与另一点，与所在直线的交点即为所求的点．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
17．对于函数y=-2x+4．下列说法错误的是（ ）
| A． | y随x的增大而减小 | B． | 它的图象与y轴的交点是（0，4） | ||
| C． | 当x＜2时，y＜0 | D． | 它的图象不经过第三象限 |
18．
一副三角板如图叠放在一起，∠α的度数为（ ）
一副三角板如图叠放在一起，∠α的度数为（ ）| A． | 95° | B． | 100° | C． | 105° | D． | 120° |
12．
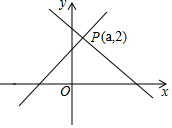如图，直线y=x+1与直线y=mx+n相交于点P（a，2），则关于不等式x+1≥mx+n的解集是（ ）
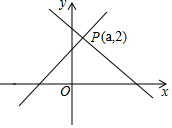如图，直线y=x+1与直线y=mx+n相交于点P（a，2），则关于不等式x+1≥mx+n的解集是（ ）| A． | x≥-1 | B． | 0≤x≤1 | C． | x≥1 | D． | x≤1 |
16．若圆锥的侧面展开图是个半圆，则该圆锥的侧面积与全面积之比为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{\sqrt{3}}{2}$ |
6．
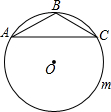如图，△ABC中，AB=BC，∠ABC=120°，AC=2$\sqrt{3}$，⊙O是△ABC的外接圆，D是优弧AmC上任意一点（不包括A，C），记四边形ABCD的周长为y，BD的长为x，则y关于x的函数关系式是（ ）
如图，△ABC中，AB=BC，∠ABC=120°，AC=2$\sqrt{3}$，⊙O是△ABC的外接圆，D是优弧AmC上任意一点（不包括A，C），记四边形ABCD的周长为y，BD的长为x，则y关于x的函数关系式是（ ）| A． | y=$\frac{\sqrt{3}}{4}$x+4 | B． | y=$\sqrt{3}$x+4 | C． | y=$\sqrt{3}$x2+4 | D． | y=$\frac{\sqrt{3}}{4}$x2+4 |