如图.在△ABC中.AB=AC.∠A=30°.以B为圆心.BC的长为半径圆弧.交AC于点D.连接BD.则∠ABD=( )A．30°B．60°C．45°D．90° 题目和参考答案——青夏教育精英家教网—

题目内容

2．

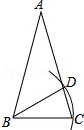如图，在△ABC中，AB=AC，∠A=30°，以B为圆心，BC的长为半径圆弧，交AC于点D，连接BD，则∠ABD=（　　）

A．

30°

B．

60°

C．

45°

D．

90°

分析先根据等腰三角形的性质和三角形的内角和求出∠ABC=∠ACB，再用三角形的外角的性质计算即可．

解答解：∵在△ABC中，AB=AC，∠A=30°，
∴∠ABC=∠ACB=75°，
又∵以B为圆心，BC的长为半径圆弧，交AC于点D，
∴∠DBC=2（90°-∠BDC）=2×（90°-75°）=30°，
又∵∠ABC=∠ABD+∠DBC，
∴∠ABD=75°-30°=45°，
故选：C．

点评此题是等腰三角形的性质，主要考查了三角形的内角和公式，三角形的外角的性质，解本题的关键是根据作图得到结论．

练习册系列答案

12．

如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+
∠ADC=180°．
（1）求证：四边形ABCD是矩形．
（2）DF⊥AC，若∠ADF：∠FDC=3：2，则∠BDF的度数是多少？

9．有下列长度的三条线段，能组成三角形的是（　　）

16．

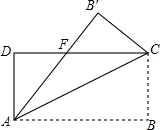如图，在矩形ABCD中，AB=8，BC=4，将矩形AC折叠，点B落在点B′处，重叠部分△AFC的面积为（　　）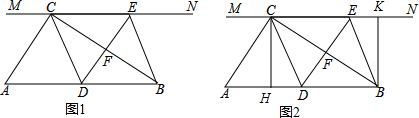

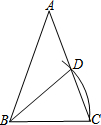7．如图1，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上的中点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
（1）四边形BECD是什么特殊四边形？说明你的理由；
（2）当∠A=45°时，四边形BECD是正方形；
（3）如图2，过点C作CH⊥AB于H，过点B作BK⊥MN于K，动点P、Q分别从C、B两点同时出发，点P自C→D→H→C停止，点Q自B→K→E→B停止，已知CD=10，CH=8，在运动过程中，点P、Q的运动路程分别为a、b（ab≠0），若C、B、P、Q四点为顶点的四边形是平行四边形，则a与b满足的数量关系式是b=24-a．

14．

如图，在△ABC中，AB=AC，∠A=36°，以B为圆心，BC为半径作弧，交AC于点D，连接BD，则∠ABD=36°．

11．

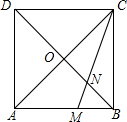如图，正方形ABCD的边长为3，对角线AC与BD相交于点O，CM交BD于点N，若BM=1，则线段ON的长为$\frac{3\sqrt{2}}{4}$．

12．如图，在平面直角坐标系xOy中，抛物线y=-$\frac{3}{8}$x²+$\frac{9}{4}$x+6与x轴交于A、B两点（点A在点B左侧），与y轴交于点C，直线l经过点A和点C，连接BC．将直线l沿着x轴正方向平移m个单位（0＜m＜10）得到直线l′，l′交x轴于点D，交BC于点E，交抛物线于点F．

（1）求点A，点B和点C的坐标；
（2）如图2，将△EDB沿直线l′翻折得到△EDB′，求点B′的坐标（用含m的代数式表示）；
（3）在（2）的条件下，当点B′落在直线AC上时，请直接写出点F的坐标．

试题分类