题目内容
16.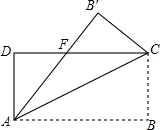 如图,在矩形ABCD中,AB=8,BC=4,将矩形AC折叠,点B落在点B′处,重叠部分△AFC的面积为( )
如图,在矩形ABCD中,AB=8,BC=4,将矩形AC折叠,点B落在点B′处,重叠部分△AFC的面积为( )| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
分析 已知AD为AF边上的高,要求△AFC的面积,求得FC即可,求证△AFD≌△CFB′,得B′F=DF,设DF=x,则在Rt△AFD中,根据勾股定理求x,于是得到CF=CD-DF,即可得到答案.
解答 解:由翻折变换的性质可知,△AFD≌△CFB′,
∴DF=BF′,
设DF=x,则AF=CF=8-x,
在Rt△AFD中,AF2=DF2+AD2,即(8-x)2=x2+42,
解之得:x=3,
∴CF=CD-FD=8-3=5,
∴S△AFC=$\frac{1}{2}$•AF•BC=10.
故选:B.
点评 本题考查了翻折变换-折叠问题,勾股定理的正确运用,本题中设DF=x,根据直角三角形AFD中运用勾股定理求x是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
6.若一个多边形的每个内角都等于135°,则该多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
7.某游乐场在暑假期间推出学生个人门票优惠价,各票价如下:
某慈善机构欲购买两种类型的票共100张奖励品学兼优的留守学生,其中购买的A种票数为x张,B种票y张.
(1)写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W与x之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不超过30张,且购票总费用不超过7160元,则有几种购票方案?并指出哪种方案费用最少.
| 票价种类 | (A)夜场通宵 | (B)白天通场 |
| 单价(元) | 50 | 80 |
(1)写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W与x之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不超过30张,且购票总费用不超过7160元,则有几种购票方案?并指出哪种方案费用最少.
2.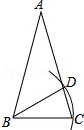 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )| A. | 30° | B. | 60° | C. | 45° | D. | 90° |
9.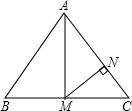 如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
 如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )| A. | $\frac{12}{5}$ | B. | $\frac{18}{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{32}{5}$ |
6.下列说法中,错误的是( )
| A. | 菱形的对角线互相平分 | B. | 正方形的对角线互相垂直平分 | ||
| C. | 矩形的对角线相等且平分 | D. | 平行四边形的对角线相等且垂直 |
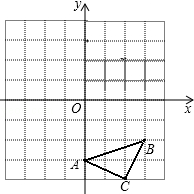 已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.
已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.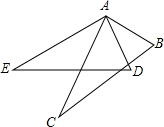 如图,已知∠BAC=∠DAE=90°,AB=AD,要使△ABC≌△ADE,还需要添加的条件是AE=AC(只需添加一个条件即可)
如图,已知∠BAC=∠DAE=90°,AB=AD,要使△ABC≌△ADE,还需要添加的条件是AE=AC(只需添加一个条件即可)