题目内容
11.平行四边形ABCD中,对角线AC、BD的长度分别为10、6,则边AB的长度取值范围是2<AB<8.分析 根据平四边形的性质,可求得OA与OB的长,再由三角形的三边关系,求得答案即可.
解答 解:如图所示:
∵?ABCD的对角线AC和BD相交于点O,AC=6,BD=4,
∴OA=$\frac{1}{2}$AC=5,OB=$\frac{1}{2}$BD=3,
∴在△AOB中,由三角形的三边关系得:5-3<AB<5+3,
即2<AB<8.
故答案为:2<AB<8.
点评 本题考查了平行四边形的性质和三角形的三边关系的综合运用;注意平行四边形的对角线互相平分..

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
6.若一个多边形的每个内角都等于135°,则该多边形的边数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
16.计算:(ab3)2=( )
| A. | a2b2 | B. | a2b3 | C. | ab6 | D. | a2b6 |
20.已知一次函数y=ax+b在平面直角坐标系中的图案经过第一、二、三象限,则下列对a、b的符号判断正确的是( )
| A. | a<0,b<0 | B. | a>0,b>0 | C. | a>0,b<0 | D. | a<0,b>0 |
2.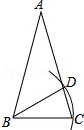 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )| A. | 30° | B. | 60° | C. | 45° | D. | 90° |
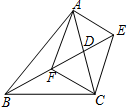 如图,在△ABC中,BD是AC边上的中线,F是BD上的一点,过点C作CE∥AF,交BD的延长线于点E.
如图,在△ABC中,BD是AC边上的中线,F是BD上的一点,过点C作CE∥AF,交BD的延长线于点E. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.