题目内容
12. 如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+
如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)DF⊥AC,若∠ADF:∠FDC=3:2,则∠BDF的度数是多少?
分析 (1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;
(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.
解答 (1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,
∴∠DCO=90°-36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC-∠FDC=18°.
点评 本题考查了平行四边形的性质和判定,矩形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键,注意:矩形的对角线相等,有一个角是直角的平行四边形是矩形.

练习册系列答案
相关题目
20.已知一次函数y=ax+b在平面直角坐标系中的图案经过第一、二、三象限,则下列对a、b的符号判断正确的是( )
| A. | a<0,b<0 | B. | a>0,b>0 | C. | a>0,b<0 | D. | a<0,b>0 |
7.某游乐场在暑假期间推出学生个人门票优惠价,各票价如下:
某慈善机构欲购买两种类型的票共100张奖励品学兼优的留守学生,其中购买的A种票数为x张,B种票y张.
(1)写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W与x之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不超过30张,且购票总费用不超过7160元,则有几种购票方案?并指出哪种方案费用最少.
| 票价种类 | (A)夜场通宵 | (B)白天通场 |
| 单价(元) | 50 | 80 |
(1)写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W与x之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不超过30张,且购票总费用不超过7160元,则有几种购票方案?并指出哪种方案费用最少.
17.若2(a+3)的值与4互为相反数,则a的值为( )
| A. | -1 | B. | -$\frac{7}{2}$ | C. | -5 | D. | $\frac{1}{2}$ |
2.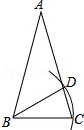 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )| A. | 30° | B. | 60° | C. | 45° | D. | 90° |
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为28°.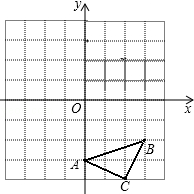 已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.
已知:如图△ABC三个顶点的坐标分别为A(0,-3)、B(3,-2)、C(2,-4),正方形网格中,每个小正方形的边长是1个单位长度.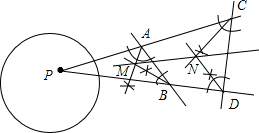 阅读下面材料:
阅读下面材料: