题目内容
6.计算:(1)3x2+5(2x+1)=0.
(2)2sin45°+2cos60°-$\sqrt{3}$tan60°+$\sqrt{18}$.
分析 (1)根据求根公式x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$进行解答;
(2)根据特殊角的三角函数值代入,然后计算加减法.
解答 解:(1)由原方程,得
3x2+10x+5=0,
则△=100-4×3×5=40,
故x=$\frac{-10±\sqrt{40}}{6}$=$\frac{-5±\sqrt{10}}{3}$,
解得x1=$\frac{-5+\sqrt{10}}{3}$,x2=$\frac{-5-\sqrt{10}}{3}$.
(2)原式=2×$\frac{\sqrt{2}}{2}$+2×$\frac{1}{2}$-$\sqrt{3}$×$\sqrt{3}$+3$\sqrt{2}$,
=$\sqrt{2}$+1-3+3$\sqrt{2}$,
=4$\sqrt{2}$-2.
点评 本题考查了解一元二次方程--公式法和特殊角的三角函数值.熟记一元二次方程的求根公式是解题的关键.

练习册系列答案
相关题目
17.从2004年8月1日起,浙江省城乡居民生活用电执行新的电价政策:安装“一户一表”的居民用户,按所抄见电量(每家用户电表所表示的用电量)实行阶梯式累进加价,收费标准如下:
例:若某户月用电300千瓦时,需交电费为
0.53×50+0.56×(200-50)+0.63×(300-200)=173.5(元)
(1)若10月份王老师家用电量为120千瓦时,则10月份王老师家应付电费多少元?
(2)已知王老师家10月份的用电量为a 千瓦时,请完成下列填空:
①若a≤50千瓦时,则10月份王老师家应付电费为0.53a 元;
②若50<a≤200千瓦时,则10月份王老师家应付电费为0.56a-1.5元;
③若a>200千瓦时,则10月份王老师家应付电费为0.63a-15.5 元.
(3)若10月份王老师家应付电费为96.50元,则10月份王老师家的用电量是多少千瓦时?
| 月用电量 | 不超过50千瓦时的部分 | 超过50千瓦时不超过200千瓦时的部分 | 超过200千瓦时的部分 |
| 收费标准(元/千瓦时) | 0.53 | 0.56 | 0.63 |
0.53×50+0.56×(200-50)+0.63×(300-200)=173.5(元)
(1)若10月份王老师家用电量为120千瓦时,则10月份王老师家应付电费多少元?
(2)已知王老师家10月份的用电量为a 千瓦时,请完成下列填空:
①若a≤50千瓦时,则10月份王老师家应付电费为0.53a 元;
②若50<a≤200千瓦时,则10月份王老师家应付电费为0.56a-1.5元;
③若a>200千瓦时,则10月份王老师家应付电费为0.63a-15.5 元.
(3)若10月份王老师家应付电费为96.50元,则10月份王老师家的用电量是多少千瓦时?
14.如果把分式$\frac{x-y}{xy}$中的x和y都扩大了3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
11.方程(x-3)(x+1)=0的根为( )
| A. | 3,1 | B. | 3,-1 | C. | -3,1 | D. | -3,-1 |
18.下列长度的三条线段,能组成三角形的是( )
| A. | 4cm、5cm、9cm | B. | 8cm、7cm、15cm | C. | 5cm、5cm、11cm | D. | 13cm、12cm、20cm |
 如图,∠ACE=∠BCF,请补充一个条件:∠A=∠E(答案不唯一),使△ACB∽△ECF.
如图,∠ACE=∠BCF,请补充一个条件:∠A=∠E(答案不唯一),使△ACB∽△ECF. 如图,已知线段AB.用尺规作图的方法作出线段AB的垂直平分线(保留作图痕迹,不要求写出作法).
如图,已知线段AB.用尺规作图的方法作出线段AB的垂直平分线(保留作图痕迹,不要求写出作法).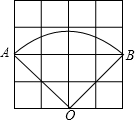 如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).
如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).