Question

15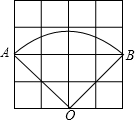．如图，在4×4的方格纸中（共有16个小方格），每个小方格都是边长为1的正方形．O、A、B分别是小正方形的顶点，求扇形OAB的弧长，周长和面积．（结果保留根号及π）．

Answer 1

分析 根据已知条件分别求出扇形的半径和扇形的圆心角的度数代入扇形弧长公式求出弧长，然后加上两条半径即可得到本题答案．

解答 解：由图形可知，∠AOB=90°，
∴OA=OB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，
∴扇形OAB的面积=$\frac{90π×（2\sqrt{2}）^{2}}{360}$=2π，弧AB的长是：$\frac{90π×2\sqrt{2}}{180}$=$\sqrt{2}$π
∴周长=弧AB的长+2OA=$\sqrt{2}$π+4$\sqrt{2}$．
综上所述，扇形OAB的弧长是$\sqrt{2}$π，周长是$\sqrt{2}$π+4$\sqrt{2}$，面积是2π．

点评 本题考查了勾股定理及弧长公式的应用．解题的关键是正确的求出扇形的圆心角及半径．