题目内容
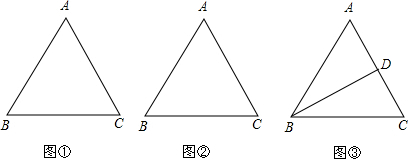
 在△ABC中,∠A=60°,∠C=75°,AB=10,D、E、F分别在AB、BC、CA上,当△DEF的周长最小值时,试确定D、E、F的位置.
在△ABC中,∠A=60°,∠C=75°,AB=10,D、E、F分别在AB、BC、CA上,当△DEF的周长最小值时,试确定D、E、F的位置.考点:轴对称-最短路线问题
专题:
分析:先过A作AE⊥BC于点E,再作点E关于AB的对称点E′,作点E关于AC的对称点E″,连接E′E″交AB于点D,交AC于点F,顺次连接即可得到所求作的△DEF.
解答:解:如图,过A作AE⊥BC,过点E分别作AB、AC的对称点E′、E″,连接E′E″交AB、AC于D、E,则△DEF为所求.


点评:本题考查了利用轴对称确定最短路线问题,其理论依据是三角形的两边之和大于第三边,作出对称点是解题的关键.

练习册系列答案
相关题目
如果六条直线两两相交,仅有三条直线过一点,则截得不重复线段有( )条.
| A、42 | B、46 | C、48 | D、50 |
a是实数,a2+1与2a的大小关系是( )
| A、a2+1≥2a |
| B、a2+1>2a |
| C、a2+1与2a的大小关系随a的变化而改变 |
| D、当a>0时,a2+1≤a;当a<0时,a2+1≥2a |
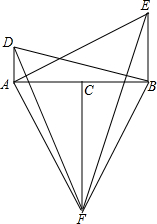 如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB.
如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB. 如图,在△ABC中,AD、CE分别为BC、AB边上高,且BE:BC=1:2,∠DAC=45°,DE=3,求△ABC三边的长.
如图,在△ABC中,AD、CE分别为BC、AB边上高,且BE:BC=1:2,∠DAC=45°,DE=3,求△ABC三边的长.