题目内容
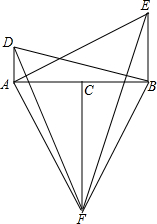 如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB.
如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB.(1)图中有哪些线段相等?为什么?
(2)线段BD与BF有怎样的关系?
(3)求∠AFE的大小;
(4)若∠AFB=51°,求∠DFE的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)图中相等线段:DA=BC,AC=BE,FC=AB.(已知)AE=AF,BD=BF,根据SAS求得△ACF≌△EBA,△ADB≌△CBF,即可求得AE=AF,BD=BF;
(2)BD=BF;
(3)先求得∠EAF,∠DBF为直角,根据AE=AF,BD=BF,求得∠AFE=45°,∠DAB=45°,进而求得∠AFD=∠BFE=51°-45°=6°,最后用∠AFE-∠AFD即可求得∠DFE的度数.
(2)BD=BF;
(3)先求得∠EAF,∠DBF为直角,根据AE=AF,BD=BF,求得∠AFE=45°,∠DAB=45°,进而求得∠AFD=∠BFE=51°-45°=6°,最后用∠AFE-∠AFD即可求得∠DFE的度数.
解答:解:(1)DA=BC,AC=BE,FC=AB.(已知)AE=AF,BD=BF,
理由:∵DA⊥AB,BE⊥AB,FC⊥AB,
∴∠ACF=∠EBA=∠BCF=∠DAB=90°,
在△ACF与△EBA中,
,
∴△ACF≌△EBA(SAS),
∴AE=AF,
同理可证△ADB≌△CBF,
∴BD=BF;
(2)BD=BF;
(3)∵△ACF≌△EBA,
∴∠CAF=∠BEA,
∵∠BEA+∠EAB=90°,
∴∠CAF+∠EAB=90°,
即∠EAF=90°,
∵AE=AF,
∴∠AFE=45°,
同理∠DAB=45°,
∴∠AFD=∠BFE,
∵∠AFB=51°,
∴∠AFD=∠BFE=51°-45°=6°,
∴∠DFE=∠AFE-∠AFD=45°-6°=39°.
理由:∵DA⊥AB,BE⊥AB,FC⊥AB,
∴∠ACF=∠EBA=∠BCF=∠DAB=90°,
在△ACF与△EBA中,
|
∴△ACF≌△EBA(SAS),
∴AE=AF,
同理可证△ADB≌△CBF,
∴BD=BF;
(2)BD=BF;
(3)∵△ACF≌△EBA,
∴∠CAF=∠BEA,
∵∠BEA+∠EAB=90°,
∴∠CAF+∠EAB=90°,
即∠EAF=90°,
∵AE=AF,
∴∠AFE=45°,
同理∠DAB=45°,
∴∠AFD=∠BFE,
∵∠AFB=51°,
∴∠AFD=∠BFE=51°-45°=6°,
∴∠DFE=∠AFE-∠AFD=45°-6°=39°.
点评:本题考查了全等三角形的判定和性质,等腰直角三角形的性质等,能够熟练掌握是关键.

练习册系列答案
相关题目
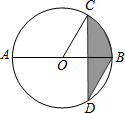 如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4
如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4| 3 |
A、
| ||
B、
| ||
| C、4π | ||
| D、8π |
 在四边形ABCD,AC与BD相交于点E,AC⊥AB,BD⊥CD,S△EBC=16,S△AED=8.求:
在四边形ABCD,AC与BD相交于点E,AC⊥AB,BD⊥CD,S△EBC=16,S△AED=8.求: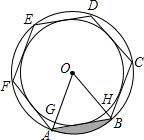 如图,两个同心圆的圆心为O,正六边形ABCDEF的顶点在大圆上,六条边分别与小圆相切,大圆的半径OA、OB分别与小圆相交于点G、H,正六边形的边长为2a.
如图,两个同心圆的圆心为O,正六边形ABCDEF的顶点在大圆上,六条边分别与小圆相切,大圆的半径OA、OB分别与小圆相交于点G、H,正六边形的边长为2a.
 在△ABC中,∠A=60°,∠C=75°,AB=10,D、E、F分别在AB、BC、CA上,当△DEF的周长最小值时,试确定D、E、F的位置.
在△ABC中,∠A=60°,∠C=75°,AB=10,D、E、F分别在AB、BC、CA上,当△DEF的周长最小值时,试确定D、E、F的位置. 已知AB∥ED,∠ABC=140°,∠BCD=80°,求∠CDE.
已知AB∥ED,∠ABC=140°,∠BCD=80°,求∠CDE. 如图,三角形ABO的面积为12,且AO=AB,双曲线y=
如图,三角形ABO的面积为12,且AO=AB,双曲线y=