题目内容
a是实数，a2+1与2a的大小关系是（ ）
| A、a2+1≥2a |
| B、a2+1＞2a |
| C、a2+1与2a的大小关系随a的变化而改变 |
| D、当a＞0时，a2+1≤a；当a＜0时，a2+1≥2a |
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：根据a2+1-2a=（a-1）2≥0，即可得出答案．
解答：解：∵a2+1-2a=（a-1）2≥0，
∴a2+1≥2a，
故选：A．
∴a2+1≥2a，
故选：A．
点评：此题考查了配方法的应用，用到的知识点是完全平方公式、非负数的性质，关键是求出a2+1-2a≥0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，∠A=60°，∠C=75°，AB=10，D、E、F分别在AB、BC、CA上，当△DEF的周长最小值时，试确定D、E、F的位置．
如图，三角形ABO的面积为12，且AO=AB，双曲线y=
如图，在△ABC中，AB=AC=20，BC=32，点D在BC上，且AD=13，试确定点D的位置．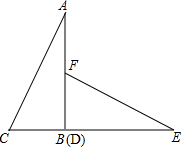
两张全等的直角三角形纸片如图摆放，期中B、D重合，B、C、E在同一条直线上，已知AB=4，BC=3，现将△DEF沿射线BC方向平行移动，在整个运动过程中，要使△ACE成为等腰三角形，求△DEF平移的距离．
如图所示，△ABC中，∠C=90°，AM平分∠CAB，BC=16cm，CM：MB=3：5，求点M到AB的距离．