题目内容
由函数y=|x2-x-2|和y=|x2-x|的图象围成一个封闭区域,则在这个封闭区域内(包括边界),纵坐标和横坐标均为整数的点共有( )个.
| A、2个 | B、4个 | C、6个 | D、8个 |
考点:y=|ax2+bx+c|的图象与性质
专题:
分析:分别画出函数y=|x2-x-2|和y=|x2-x|的图象,进而得出符合题意的点.
解答: 解:如图所示:由函数y=|x2-x-2|和y=|x2-x|的图象围成一个封闭区域,
解:如图所示:由函数y=|x2-x-2|和y=|x2-x|的图象围成一个封闭区域,
则在这个封闭区域内(包括边界),纵坐标和横坐标均为整数的点共有:(0,2),(0,1),(0,0),(1,0),(1,1),(1,2)一共有6个点.
故选:C.
 解:如图所示:由函数y=|x2-x-2|和y=|x2-x|的图象围成一个封闭区域,
解:如图所示:由函数y=|x2-x-2|和y=|x2-x|的图象围成一个封闭区域,则在这个封闭区域内(包括边界),纵坐标和横坐标均为整数的点共有:(0,2),(0,1),(0,0),(1,0),(1,1),(1,2)一共有6个点.
故选:C.
点评:此题主要考查了y=|ax2+bx+c|的图象与性质,根据题意画出正确图象是解题关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
下列运动属于平移的是( )
| A、荡秋千 |
| B、急刹车时,汽车在地面上的滑动 |
| C、风筝在空中随风飘动 |
| D、地球绕着太阳转 |
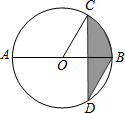 如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4
如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4| 3 |
A、
| ||
B、
| ||
| C、4π | ||
| D、8π |
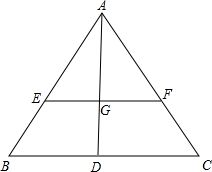 已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB、AC于点E、F.求AF:FC和EF:BC的值.
已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB、AC于点E、F.求AF:FC和EF:BC的值. 在△ABC中,∠A=60°,∠C=75°,AB=10,D、E、F分别在AB、BC、CA上,当△DEF的周长最小值时,试确定D、E、F的位置.
在△ABC中,∠A=60°,∠C=75°,AB=10,D、E、F分别在AB、BC、CA上,当△DEF的周长最小值时,试确定D、E、F的位置.