题目内容
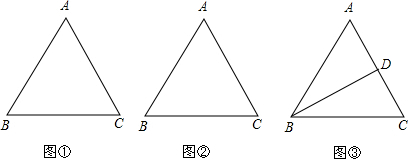
某县为了加快新农村的建设由供水公司为农村建造自来水,从而改善农村用水问题.某镇有三个村庄A、B、C正好位于一个等边三角形的三个顶点,每两个村庄相距akm,现计划在三个村庄联合架设一条铺设水管的线路,共设计了三种方案:
第一套方案:△ABC内找一点O,使它到△ABC的三个顶点A、B、C的距离相等;
第二套方案:如图②,按线路A--B--C进行铺设;
第三套方案:如图③,点D为AC的中点,按A--D、D--B、D--C的线路进行铺设.?
(1)在图①中用尺规作图的方法作出点O;?
(2)求出方案一所需铺设水管的长度;
(3)你帮忙计算一下,哪种方案最省水管.
第一套方案:△ABC内找一点O,使它到△ABC的三个顶点A、B、C的距离相等;
第二套方案:如图②,按线路A--B--C进行铺设;
第三套方案:如图③,点D为AC的中点,按A--D、D--B、D--C的线路进行铺设.?
(1)在图①中用尺规作图的方法作出点O;?
(2)求出方案一所需铺设水管的长度;
(3)你帮忙计算一下,哪种方案最省水管.

考点:轴对称-最短路线问题
专题:
分析:(1)由于三角形的外心是三角形三边中垂线的交点,可作△ABC的任意两边的垂直平分线,它们的交点即为△ABC的外接圆的圆心;
(2)、(3)根据等边三角形的性质分别求出三个图形中的电线长度,然后判断大小即可.
(2)、(3)根据等边三角形的性质分别求出三个图形中的电线长度,然后判断大小即可.
解答: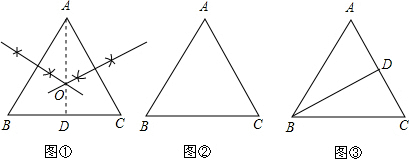 解:(1)△ABC的外接圆圆心到△ABC的三个顶点A、B、C的距离相等,可作△ABC的任意两边的垂直平分线,它们的交点即为△ABC的外接圆的圆心O,如图①所示.
解:(1)△ABC的外接圆圆心到△ABC的三个顶点A、B、C的距离相等,可作△ABC的任意两边的垂直平分线,它们的交点即为△ABC的外接圆的圆心O,如图①所示.
(2)依题意知,△ABC是等边三角形.
如图①,延长AO交BC于点D.则
水管的长度为:3×
=3×
=
a;
(3)图②中水管的长度是3a.
图③中水管的长度是:a+a•sin60°=a+a×
=
a.
由(2)知.图①中水管的长度是
a.
∵3a>
a>
a,
∴方案一最省钱.
 解:(1)△ABC的外接圆圆心到△ABC的三个顶点A、B、C的距离相等,可作△ABC的任意两边的垂直平分线,它们的交点即为△ABC的外接圆的圆心O,如图①所示.
解:(1)△ABC的外接圆圆心到△ABC的三个顶点A、B、C的距离相等,可作△ABC的任意两边的垂直平分线,它们的交点即为△ABC的外接圆的圆心O,如图①所示.(2)依题意知,△ABC是等边三角形.
如图①,延长AO交BC于点D.则
水管的长度为:3×
| CD |
| cos30° |
| ||
| cos30° |
| 3 |
(3)图②中水管的长度是3a.
图③中水管的长度是:a+a•sin60°=a+a×
| ||
| 2 |
2+
| ||
| 2 |
由(2)知.图①中水管的长度是
| 3 |
∵3a>
2+
| ||
| 2 |
| 3 |
∴方案一最省钱.
点评:本题考查了等边三角形的性质以及锐角三角函数.解答(1)题时,能找到等边三角形的外接圆圆心是解题的难点.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 在△ABC中,∠A=60°,∠C=75°,AB=10,D、E、F分别在AB、BC、CA上,当△DEF的周长最小值时,试确定D、E、F的位置.
在△ABC中,∠A=60°,∠C=75°,AB=10,D、E、F分别在AB、BC、CA上,当△DEF的周长最小值时,试确定D、E、F的位置. 已知AB∥ED,∠ABC=140°,∠BCD=80°,求∠CDE.
已知AB∥ED,∠ABC=140°,∠BCD=80°,求∠CDE. 如图,直线y=x-1与反比例函数y=
如图,直线y=x-1与反比例函数y=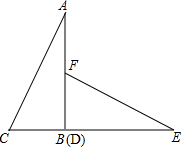 两张全等的直角三角形纸片如图摆放,期中B、D重合,B、C、E在同一条直线上,已知AB=4,BC=3,现将△DEF沿射线BC方向平行移动,在整个运动过程中,要使△ACE成为等腰三角形,求△DEF平移的距离.
两张全等的直角三角形纸片如图摆放,期中B、D重合,B、C、E在同一条直线上,已知AB=4,BC=3,现将△DEF沿射线BC方向平行移动,在整个运动过程中,要使△ACE成为等腰三角形,求△DEF平移的距离.