题目内容
2.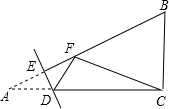 如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.
如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.
分析 由勾股定理求出AB,设AE=x,则EF=x,BF=10-2x;分三种情况讨论:
①当BF=BC时,列出方程,解方程即可;
②当BF=CF时,F在BC的垂直平分线上,得出AF=BF,列出方程,解方程即可;
③当CF=BC时,作CG⊥AB于G,则BG=FG=$\frac{1}{2}$BF,由射影定理求出BG,再解方程即可.
解答 解:由翻折变换的性质得:AE=EF,
∵∠ACB=90°,AC=8,BC=6,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
设AE=EF=x,则BF=10-2x;
分三种情况讨论:
①当BF=BC时,10-2x=6,
解得:x=2,
∴AE=2;
②当BF=CF时,F在BC的垂直平分线上,
∴F为AB的中点,
∴AF=BF,
∴x+x=10-2x,
解得:x=$\frac{5}{2}$,
∴AE=$\frac{5}{2}$;
③当CF=BC时,作CG⊥AB于G,如图所示: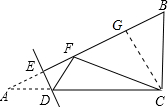 则BG=FG=$\frac{1}{2}$BF,
则BG=FG=$\frac{1}{2}$BF,
根据射影定理得:BC2=BG•AB,
∴BG=$\frac{B{C}^{2}}{AB}$=$\frac{{6}^{2}}{10}$=$\frac{18}{5}$,
即$\frac{1}{2}$(10-2x)=$\frac{18}{5}$,
解得:x=$\frac{7}{5}$,
∴AE=$\frac{7}{5}$;
综上所述:当△BCF为等腰三角形时,AE的长为:2或$\frac{5}{2}$或$\frac{7}{5}$;
故答案为:2或$\frac{5}{2}$或$\frac{7}{5}$.
点评 本题考查了翻折变换的性质、线段垂直平分线的性质、勾股定理、射影定理、等腰三角形的性质;本题有一定难度,需要进行分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若$\frac{a+b}{c}$=$\frac{b+c}{a}$=$\frac{a+c}{b}$=k,则一次函数y=kx+x必经过( )
| A. | 第一、二象限 | B. | 第二、三象限 | C. | 第三、四象限 | D. | 第一、四象限 |
15.已知等腰三角形的两边长分别为5cm、3cm,则该等腰三角形的周长是( )
| A. | 13cm | B. | 11cm | C. | 13cm或者11cm | D. | 8cm |
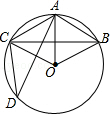 如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°.
如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°.
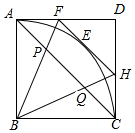 如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H.
如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H.  如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.