题目内容
17.定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数[2m,1-m,-1-m]的函数的一些结论:①当m=-3时,函数图象的顶点坐标是($\frac{1}{3}$,$\frac{8}{3}$);②当m=2时,函数图象的对称轴方程是x=-$\frac{1}{8}$;③当m>0时,函数图象截x轴所得的线段长度大于$\frac{3}{2}$;④当m<0时,函数在x<$\frac{1}{4}$时,y随x的增大而增大.其中正确的结论有①③④.(请填写所有正确的序号)
分析 ①把m=-3代入[2m,1-m,-1-m],求得[a,b,c],求得解析式,利用顶点坐标公式解答即可;
②首先求得对称轴,比较即可;
③令函数值为0,求得与x轴交点坐标,利用两点间距离公式解决问题;
④首先求得对称轴,利用二次函数的性质解答即可;
解答 解:因为函数y=ax2+bx+c的特征数为[2m,1-m,-1-m];
①当m=-3时,y=-6x2+4x+2=-6(x-$\frac{1}{3}$)2+$\frac{8}{3}$,顶点坐标是($\frac{1}{3}$,$\frac{8}{3}$);此结论正确;
②当m=2时,y=4x2-x-3的对称轴是x=$\frac{1}{8}$,此结论错误;
③当m>0时,令y=0,有2mx2+(1-m)x+(-1-m)=0,解得x=$\frac{(m-1)±(m+3)}{4m}$,x1=1,x2=-$\frac{1}{2}$-$\frac{1}{2m}$,
|x2-x1|=$\frac{3}{2}$+$\frac{1}{2m}$>$\frac{3}{2}$,所以当m>0时,函数图象截x轴所得的线段长度大于$\frac{3}{2}$,此结论正确;
④当m<0时,y=2mx2+(1-m)x+(-1-m) 是一个开口向下的抛物线,其对称轴是:$\frac{m-1}{4m}$,在对称轴的左边y随x的增大而增大,因为当m<0时,$\frac{m-1}{4m}$=$\frac{1}{4}$-$\frac{1}{4m}$>$\frac{1}{4}$,即对称轴在x=$\frac{1}{4}$右边,因此函数在x=$\frac{1}{4}$左边y随x的增大而增大,此结论正确,
故答案为:①③④.
点评 此题考查了二次函数的性质,顶点坐标,两点间的距离公式,以及二次函数图象上点的坐标特征熟记二次函数的性质是解题的关键.

 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案| A. | (3,-2) | B. | (1,-6) | C. | (2,-3) | D. | (-1,-6) |
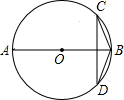 如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )| A. | 28° | B. | 34° | C. | 44° | D. | 56° |
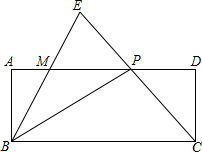 已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y
已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y 如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处.若△AEF∽△FEC∽△DFC,则$\frac{AB}{BC}$的值是$\frac{\sqrt{3}}{2}$.
如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处.若△AEF∽△FEC∽△DFC,则$\frac{AB}{BC}$的值是$\frac{\sqrt{3}}{2}$.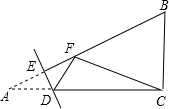 如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.
如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.