题目内容
13.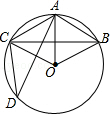 如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°.
如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°.(1)求弦BC的长及sin∠AOB的值;
(2)求证:四边形ABOC是菱形.
分析 (1)求得∠AOB的度数即可利用特殊角的三角函数值求得其正弦值,然后解直角三角形即可求得BC的长;
(2)证得AB=BO=OC=CA后利用四条边相等的四边形是菱形即可进行证明.
解答 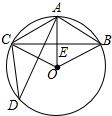 (1)解:设BC与AO交于点E.
(1)解:设BC与AO交于点E.
∵点A是劣弧$\widehat{BC}$的中点,OA过圆心,
∴$\widehat{AC}$=$\widehat{AB}$,OA⊥BC.
∴∠D=∠ACB=30°.
∴∠AOB=2∠ACB=60°.
∴sin∠AOB=sin 60°=$\frac{\sqrt{3}}{2}$.
在Rt△OBE中,OB=6 cm,
BE=OB•sin∠AOB=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$(cm),
∴BC=2BE=6$\sqrt{3}$cm.
(2)证明:∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形.
∴AB=OB.
∵点A是劣弧BC的中点,
∴AC=AB.
∴AB=BO=OC=CA.
∴四边形ABOC是菱形.
点评 本题考查了垂径定理、菱形的判定、圆周角定理、解直角三角形等知识,熟练应用菱形的判定方法是解题关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
8.若正比例函数y=kx(k≠0)的图象经过点P(-2,3),则该函数的图象经过的点是( )
| A. | (3,-2) | B. | (1,-6) | C. | (2,-3) | D. | (-1,-6) |
18.若不等式组$\left\{\begin{array}{l}{\frac{5x-3}{3}+3>x}\\{x≤a}\end{array}\right.$的整数解有四个,则a的取值范围是( )
| A. | a≥1 | B. | 1<a≤2 | C. | 1≤a<2 | D. | 1<a<2 |
3.使二次根式$\sqrt{x-1}$的有意义的x的取值范围是( )
| A. | x>0 | B. | x>1 | C. | x≥1 | D. | x≠1 |
 如图,在△ABC中,AB=AC,∠BAC=50°,D是BC边的中点,连接AD,则∠BAD=25°.
如图,在△ABC中,AB=AC,∠BAC=50°,D是BC边的中点,连接AD,则∠BAD=25°.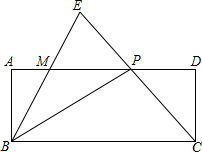 已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y
已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y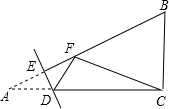 如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.
如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.