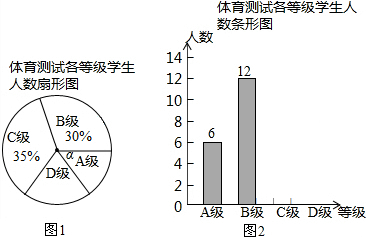
题目内容
14.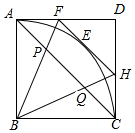 如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H.
如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H. (1)求△DFH的周长;
(2)求证:∠FBH=45°;
(3)设正方形的对角线AC交BF于P,交BH于Q,如果AP=x,CQ=y,求y与x之间满足的关系.
分析 (1)根据正方形性质得出AB⊥AD,BC⊥CD,推出DA和CD都是圆B的切线,根据切线长定理可得出FE=FA,HE=HC,代入求出即可;
(2)首先利用切线的性质得BE⊥FH,易得Rt△ABF≌Rt△EBF,Rt△EBH≌Rt△CBH,由全等三角形的性质得∠ABF=∠EBF,∠EBH=∠CBH,证得∠FBH=45°;
(3)首先利用外角的性质得∠ABQ=∠CPB,易得△ABQ∽△CPB,利用相似三角形的性质得AB:CP=AQ:CB,代入整理即可.
解答 (1)解:∵四边形ABCD为正方形,
∴∠DAB=∠D=∠DCB=90°,
即AB=BC=CD=AD,AB⊥AD,BC⊥CD,
∴DA和CD都是圆B的切线,
∵FH切圆B于E,
∴FE=FA,HE=HC,
∴△DFH的周长是DF+FE+HE+DH=DF+FA+HC+DH=AD+CD=2$\sqrt{2}$;
(2)证明:连接BE,
∵FH是圆B的切线,
∴BE⊥FH,
∴∠FEB=∠HEB=90°,
在Rt△ABF与Rt△EBF中,
$\left\{\begin{array}{l}{FA=FE}\\{FB=FB}\end{array}\right.$,
∴Rt△ABF≌Rt△EBF(HL),
∴∠ABF=∠EBF,
在Rt△EBH与Rt△CBH中,
$\left\{\begin{array}{l}{BH=BH}\\{EH=CH}\end{array}\right.$,
∴Rt△EBH≌Rt△CBH,
∴∠EBH=∠CBH,
∵∠ABC=∠ABF+∠EBF+∠EBH+∠CBH=90°,
∴$∠FBH=∠EBF+∠EBH=\frac{1}{2}∠ABC=45°$;
(3)解:∵∠CPB=∠BAC+∠ABP,∠ABQ=∠ABP+∠PBQ,∠BAC=∠PBQ=45°,
∴∠ABQ=∠CPB,
∵∠BAC=∠ACB=45°,
∴△ABQ∽△CPB,
∴AB:CP=AQ:CB,
∵AB=BC=$\sqrt{2}$,AC=2,CP=2-y,AQ=2-x,
∴$\sqrt{2}$:(2-y)=(2-x):$\sqrt{2}$,
所以X与y之间的关系为 (2-x)(2-y)=2 或y=$\frac{2x-2}{x-2}$.
点评 本题主要考查了勾股定理,切线的判定,切线长定理,相似三角形的性质和判定,正方形的性质等知识点的运用,能综合运用这些性质进行推理和计算是解此题的关键.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案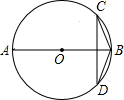 如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )| A. | 28° | B. | 34° | C. | 44° | D. | 56° |
| A. | -10 | B. | -11 | C. | 55 | D. | 10 |
| A. | x>0 | B. | x>1 | C. | x≥1 | D. | x≠1 |
| A. | k1+k2<0 | B. | k1+k2>0 | C. | k1k2<0 | D. | k1k2>0 |
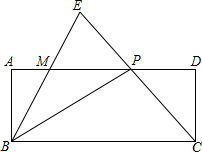 已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y
已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y 如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.
如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.