题目内容
11. 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
分析 (1)由正方形的性质得出AB=AD,∠B=90°,AD∥BC,得出∠AMB=∠EAF,再由∠B=∠AFE,即可得出结论;
(2)由勾股定理求出AM,得出AF,由△ABM∽△EFA得出比例式,求出AE,即可得出DE的长.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,
∴AM=$\sqrt{1{2}^{2}+{5}^{2}}$=13,AD=12,
∵F是AM的中点,
∴AF=$\frac{1}{2}$AM=6.5,
∵△ABM∽△EFA,
∴$\frac{BM}{AF}=\frac{AM}{AE}$,
即$\frac{5}{6.5}=\frac{13}{AE}$,
∴AE=16.9,
∴DE=AE-AD=4.9.
点评 本题考查了正方形的性质、相似三角形的判定与性质、勾股定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知方程x2-5x-1=0的两根分别为x1与x2,则2x12-x1x2+2x22=( )
| A. | -10 | B. | -11 | C. | 55 | D. | 10 |
3.使二次根式$\sqrt{x-1}$的有意义的x的取值范围是( )
| A. | x>0 | B. | x>1 | C. | x≥1 | D. | x≠1 |
 如图,在△ABC中,AB=AC,∠BAC=50°,D是BC边的中点,连接AD,则∠BAD=25°.
如图,在△ABC中,AB=AC,∠BAC=50°,D是BC边的中点,连接AD,则∠BAD=25°. 如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.
如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.
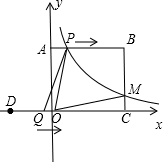 如图,平面直角坐标系(单位:cm)中,B(5,4),D(-3,0),过B作BC⊥x轴于C,BA⊥y轴于A,点P从点A出发,以每秒1cm的速度沿A→B方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿D→C方向向终点C运动,已知动点P、Q同时出发,当点P,点Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒.
如图,平面直角坐标系(单位:cm)中,B(5,4),D(-3,0),过B作BC⊥x轴于C,BA⊥y轴于A,点P从点A出发,以每秒1cm的速度沿A→B方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿D→C方向向终点C运动,已知动点P、Q同时出发,当点P,点Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒.