题目内容
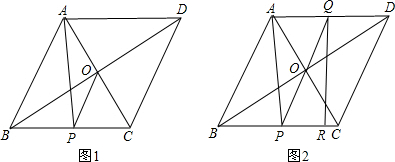
10.(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠ECG=45°,求证:S△ECG=S△BCE+S△CDG.

分析 (1)先利用正方形的性质得到CB=CD,∠B=∠ADC=90°,然后根据“SAS”证明△CBE≌△CDF,则可根据全等三角形的性质得到CE=CF;
(2)延长AD到F,使DF=BE,连结CF,如图2,由(1)得△CBE≌△CDF,则CE=CF,∠1=∠2,S△BCE=S△CDF,利用∠1+∠DCE=90°可得∠2+∠DCE=90°,所以∠ECG=∠FCG=45°,则可利用“SAS”证明△CEG≌△CFG,则S△ECG=S△CFG,易得S△ECG=S△BCE+S△CDG.
解答 (1)证明:∵四边形ABCd为正方形,
∴CB=CD,∠B=∠ADC=90°,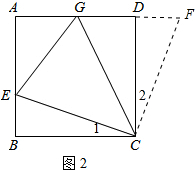
在△CBE和△CDF中
$\left\{\begin{array}{l}{BE=DF}\\{∠CBE=∠CDF}\\{CB=CD}\end{array}\right.$,
∴△CBE≌△CDF,
∴CE=CF;
(2)证明:延长AD到F,使DF=BE,连结CF,如图2,
由(1)得△CBE≌△CDF,
∴CE=CF,∠1=∠2,S△BCE=S△CDF,
∵∠1+∠DCE=90°,
∴∠2+∠DCE=90°,即∠ECF=90°,
∵∠ECG=45°,
∴∠FCG=45°,
在△CEG和△CFG中,
$\left\{\begin{array}{l}{CE=CF}\\{∠ECG=∠FCG}\\{CG=CG}\end{array}\right.$,
∴△CEG≌△CFG,
∴S△ECG=S△CFG,
∴S△ECG=S△CDF+S△CDG=S△BCE+S△CDG.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了正方形的性质.在解决(2)时要运用(1)的结论.

 阅读快车系列答案
阅读快车系列答案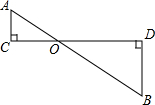 如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )
如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )| A. | 只有1个 | B. | 可以有2个 | C. | 可以有3个 | D. | 有无数个 |
| A. | a≥1 | B. | 1<a≤2 | C. | 1≤a<2 | D. | 1<a<2 |
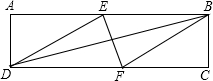 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
②若DE2=BD•EF,则DF=2AD.
那么,下面判断正确的是( )
| A. | ①是真命题,②是真命题 | B. | ①是真命题,②是假命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①假命题,②假命题 |
| A. | -10 | B. | -11 | C. | 55 | D. | 10 |
 如图,在△ABC中,AB=AC,∠BAC=50°,D是BC边的中点,连接AD,则∠BAD=25°.
如图,在△ABC中,AB=AC,∠BAC=50°,D是BC边的中点,连接AD,则∠BAD=25°.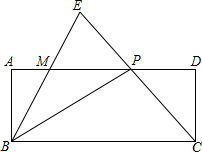 已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y
已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y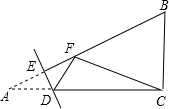 如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.
如图,在Rt△ABC中,/ACB=90°,AC=8,BC=6,点E是AB边上一动点,过点E作DE⊥AB交AC边于点D,将∠A沿直线DE翻折,点A落在线段AB上的F处,连接FC,当△BCF为等腰三角形时,AE的长为2或$\frac{5}{2}$或$\frac{7}{5}$.