题目内容
设a=
,b=
,c=
,且x+y+z≠0,则
+
+
= .
| x |
| y+z |
| y |
| z+x |
| z |
| x+y |
| a |
| a+1 |
| b |
| b+1 |
| c |
| c+1 |
考点:对称式和轮换对称式
专题:
分析:∵a=
,b=
,c=
分别代入
,
,
表示出
,
,
的值,然后化简就可以求出结果了.
| x |
| y+z |
| y |
| z+x |
| z |
| x+y |
| a |
| a+1 |
| b |
| b+1 |
| c |
| c+1 |
| a |
| a+1 |
| b |
| b+1 |
| c |
| c+1 |
解答:解:∵a=
,b=
,c=
,
∴
=
=
=
∴
+
+
=
+
+
=
∵x+y+z≠0
∴原式=1.
故答案为:1.
| x |
| y+z |
| y |
| z+x |
| z |
| x+y |
∴
| a |
| a+1 |
| x |
| x+y+z |
| b |
| b+1 |
| y |
| x+y+z |
| c |
| c+1 |
| z |
| x+y+z |
∴
| a |
| a+1 |
| b |
| b+1 |
| c |
| c+1 |
| x |
| x+y+z |
| y |
| x+y+z |
| z |
| x+y+z |
=
| x+y+z |
| x+y+z |
∵x+y+z≠0
∴原式=1.
故答案为:1.
点评:本题是一道代数式的化简求值的题,考查了代数式的对称式和轮换对称式在化简求值中的运用.具有一定的难度.

练习册系列答案
相关题目
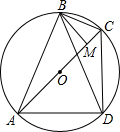 如图:已知点A、B、C、D顺次在圆O上,AB=BD,BM⊥AC,垂足为M.证明:AM=DC+CM.(阿基米德折弦定理)
如图:已知点A、B、C、D顺次在圆O上,AB=BD,BM⊥AC,垂足为M.证明:AM=DC+CM.(阿基米德折弦定理) 公园小路如图,只要把A,B,C,D,E,F,G七个点中的
公园小路如图,只要把A,B,C,D,E,F,G七个点中的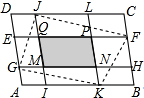 如图,在平行四边形ABCD中,EF∥GH∥AB,IJ∥KL∥BC,若四边形MNPQ的面积为19,四边形GKFL的面积为90,则平行四边形ABCD的面积为
如图,在平行四边形ABCD中,EF∥GH∥AB,IJ∥KL∥BC,若四边形MNPQ的面积为19,四边形GKFL的面积为90,则平行四边形ABCD的面积为 如图,△ABC中,MN∥BC,IJ∥AC,EF∥AB,若平行四边形BFPM,CNPJ的面积分别为70,30,△ABC的面积为225,则平行四边形AEPI的面积为
如图,△ABC中,MN∥BC,IJ∥AC,EF∥AB,若平行四边形BFPM,CNPJ的面积分别为70,30,△ABC的面积为225,则平行四边形AEPI的面积为