Question

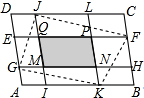如图，在平行四边形ABCD中，EF∥GH∥AB，IJ∥KL∥BC，若四边形MNPQ的面积为19，四边形GKFL的面积为90，则平行四边形ABCD的面积为

 

．

Answer 1

考点：面积及等积变换,平行四边形的性质

专题：数形结合

分析：先判断出四边形DJMG、LNHC、GNKA、FPKB均为平行四边形，从而根据S_JGKF-S_MNPQ=S_KJQ+S_JGM+S_JKN+S_KFP可求出S_DJG+S_GAK+S_KBF+S_FCJ的值，进而根据S_ABCD=S_DJG+S_GAK+S_KBF+S_FCJ+S_JGKF可得出答案．

解答：解：由题意可得，四边形DJMG、LNHC、GNKA、FPKB均为平行四边形，
又∵S_JGKF-S_MNPQ=S_KJQ+S_JGM+S_JKN+S_KFP=71，
∴S_DJG+S_GAK+S_KBF+S_FCJ=71，
故S_ABCD=S_DJG+S_GAK+S_KBF+S_FCJ+S_JGKF=71+90=161．
故答案为：161．

点评：此题考查了面积及等积变换及平行四边形的性质，本题的关键之处在于掌握平行四边形的对角线平分平行四边形的面积，难度一般，注意仔细观察图形．