Question

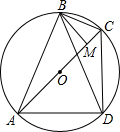如图：已知点A、B、C、D顺次在圆O上，AB=BD，BM⊥AC，垂足为M．证明：AM=DC+CM．（阿基米德折弦定理）

Answer 1

考点：旋转的性质,全等三角形的判定与性质,圆周角定理

专题：证明题

分析：如图，将△ABM绕点B旋转到△DBN，使∠BAM与∠BDC重合，再证△BMC≌△BNC，可得MC=CN，即可得出．

解答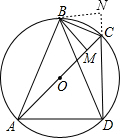：证明：∵

BC

=

BC

，
∴∠BAM=∠BDC，又AB=BD，
将△ABM绕点B旋转到△DBN，使∠BAM与∠BDC重合，如图，
∴△ABM≌△DBN，
∴AM=DN，BM=BN，∠AMB=∠N，
∵BM⊥AC，即∠AMB=90°，
∴∠N=90°，
在直角△BMC和直角△BNC中，

BM=BN BC=BC

，
∴△BMC≌△BNC，
∴CM=CN，
∴DN=CD+CN，
∴AM=DC+CM．

点评：本题主要考查了旋转的性质和全等三角形的判定与性质，通过旋转构建全等三角形，是解答的本题的关键．