题目内容
15.妈妈买回6个粽子,其中1个花生馅,2个肉馅,3个枣馅.从外表看,6个粽子完全一样,女儿有事先吃.(1)若女儿只吃一个粽子,则她吃到肉馅的概率是$\frac{1}{3}$;
(2)若女儿只吃两个粽子,求她吃到一个枣馅、一个肉馅的概率.
分析 (1)运用古典概率,有六种相等可能的结果,出现鲜肉馅粽子有两种结果,根据概率公式,即可求解;
(2)此题可以认为有两步完成,所以可以采用树状图法或者采用列表法;注意题目属于不放回实验,利用列表法即可求解.
解答 解:(1)她吃到肉馅的概率是$\frac{2}{1+2+3}$=$\frac{1}{3}$;
故答案为:$\frac{1}{3}$;
(2)如图所示:根据树状图可得,一共有30种等可能的情况,吃两个粽子,一个枣馅、一个肉馅只有12种情况,所以她吃到一个枣馅、一个肉馅的概率=$\frac{12}{30}$=$\frac{2}{5}$.
点评 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,注意是否是放回还是不放回事件是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.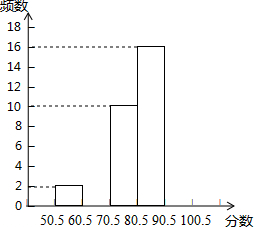 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
(1)频数分布表中A=80.5,B=16,C=0.2;
(2)补全频数分布直方图;
(3)若成绩在90分以上(不含90分)为优秀,试估计该校成绩优秀的有多少人?
 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)| 分组 | 频数 | 频率 |
| 50.5~60.5 | 2 | 0.04 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | C |
| A~90.5 | B | 0.32 |
| 90.5~100.5 | 14 | 0.28 |
| 合计 |
(2)补全频数分布直方图;
(3)若成绩在90分以上(不含90分)为优秀,试估计该校成绩优秀的有多少人?
6.某班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| |x| | |x|=4 | |x|=3 | 1≤|x|<3 |
(2)是否每次抽奖都会获奖,为什么?
4.二元一次方程组$\left\{\begin{array}{l}{x+y=5}\\{2x-y=4}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ |
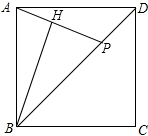 已知正方形ABCD的边长是2,点P从点D出发沿DB向点B运动,至点B停止运动,连结AP,过点B作BH⊥AP于点H,在点P运动过程中,点H所走过的路径长是π.
已知正方形ABCD的边长是2,点P从点D出发沿DB向点B运动,至点B停止运动,连结AP,过点B作BH⊥AP于点H,在点P运动过程中,点H所走过的路径长是π.