题目内容
7.已知a、b、c均为实数,且$\sqrt{a-2}$+|b+1|+(c+3)2=0,方程ax2+bx+c=0的根是x1=-1,x2=$\frac{3}{2}$.分析 直接利用非负数的性质得出a,b,c的值,进而代入方程求出答案.
解答 解:∵$\sqrt{a-2}$+|b+1|+(c+3)2=0,
∴a=2,b=-1,c=-3,
∴ax2+bx+c=0可整理为:2x2-x-3=0,
则(x+1)(2x-3)=0,
解得:x1=-1,x2=$\frac{3}{2}$.
故答案为:x1=-1,x2=$\frac{3}{2}$.
点评 此题主要考查了非负数的性质以及一元二次方程的解法,正确掌握十字相乘法解方程是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
16.$\frac{1}{2016}$的倒数是( )
| A. | -$\frac{1}{2016}$ | B. | $\frac{1}{2016}$ | C. | 2016 | D. | -2016 |

 如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA=$\frac{\sqrt{3}}{3}$,抛物线y=ax2-ax-a经过点B(2,$\sqrt{3}$),与y轴交于点D.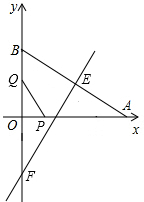 如图,在Rt△AOB中,∠AOB=90°,AO=$\sqrt{3}$,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F,点P从点A出发沿射线AO以每秒2$\sqrt{3}$个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动,设运动的时间为t秒.
如图,在Rt△AOB中,∠AOB=90°,AO=$\sqrt{3}$,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F,点P从点A出发沿射线AO以每秒2$\sqrt{3}$个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动,设运动的时间为t秒.