��Ŀ����
3����ƽ��ֱ������ϵ�У�������y=x2+��k-1��x-k��ֱ��y=kx+1����A��B���㣬��A�ڵ�B����࣮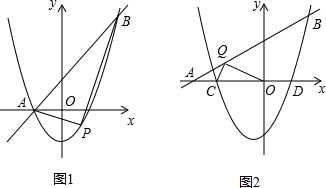
��1����ͼ1�����B������Ϊ��2��3������ôk=1��A������Ϊ��-1��0����
��2���ڣ�1���������£���PΪ�������ϵ�һ�����㣬����ֱ��AB�·����������ABP��������ֵ����ʱ��P�����ꣻ
��3����ͼ��������y=x2+��k-1��x-k��k��0����x�ύ��C��D���㣨��C�ڵ�D����ࣩ����ֱ��y=kx+1���Ƿ����Ψһһ��Q��ʹ�á�OQC=90�㣿�����ڣ��������ʱk��ֵ���������ڣ���˵�����ɣ�
���� ��1���ѣ�2��3����������һ����������ʽ�������k��ֵ����������ߵĽ���ʽ����y=0���룬���x��ֵ���������A�����ꣻ
��2������P��x��Ĵ��ߣ�����ΪD�ҽ�AB�ڵ�E������B��BF��x���ڵ�F�����P�ĺ�����Ϊa��Ȼ��ֱ����PE��AF�ij��ȣ����ԡ�ABP�����Ϊ$\frac{1}{2}$PE•AF�����ö��κ��������ʼ��������ABP��������ֵ��
��3����ֱ��y=kx+1���Ƿ����Ψһһ��Q��ʹ�á�OQC=90�㣬����COΪֱ����Բ��ֱ��AB���У���ʱ�е�ΪQ���������������ε��������AQ�ij��ȣ����������߳��������ɶ����������AO�ij��ȣ��Ӷ����k��ֵ��
��� �⣺��1����B��2��3������y=x2+��k-1��x-k��
��3=4+2��k-1��-k
��k=1��
�������ߵĽ���ʽΪy=x2-1��
��y=0����y=x2-1��
��x=��1��
��A��������-1��0����
�ʴ�Ϊ��1�� A��-1��0����
��2������P��x��Ĵ��ߣ�����ΪD�ҽ�AB�ڵ�E��
����B��BF��x���ڵ�F����ͼ1��
���ɣ�1����֪��k=1��
��ֱ��AB�Ľ���ʽΪy=x+1��
��B��2��3����
��F��2��0����
��P��������a��a2-1����-1��a��2��
��ABP�����ΪS��
��E�ĺ�����Ϊa��
��x=a����y=x+1��
��y=a+1��
��E��������a��a+1����
��PE=��a+1��-��a2-1��=-a2+a+2��
��S=$\frac{1}{2}$PE•OD+$\frac{1}{2}$PE•DF
=$\frac{1}{2}$PE•AF
=$\frac{3}{2}$��-a2+a+2��
=-$\frac{3}{2}$��a-$\frac{1}{2}$��2+$\frac{27}{8}$
��a=$\frac{1}{2}$ʱ��S�����ֵΪ$\frac{27}{8}$��
��ʱ��P��$\frac{1}{2}$��$-\frac{3}{4}$���� ��3����COΪֱ��������M��
��3����COΪֱ��������M��
��ֱ��AB���M����ʱ��
��ʱ��ֱ��y=kx+1���Ƿ����Ψһһ��Q��ʹ�á�OQC=90�㣬���е�ΪQ��
����QM����ͼ2
��y=0����y=x2+��k-1��x-k��
��ã�x=-k��x=1��
��C��-k��0��
��ֱ��AB��y�ύ�ڵ�G��
��x=0����y=kx+1��
��x=-$\frac{1}{k}$
��A��-$\frac{1}{k}$��0����
��x=0����y=kx+1
��y=1��
��G��0��1����
��OG=1��AO=$\frac{1}{k}$��OC=k��
�ߡ�MQA=��AOG=90�㣬
��GAO=��GAO��
���QAM�ס�OAG��
��$\frac{QM}{OG}$=$\frac{AQ}{AO}$��
��QM=$\frac{1}{2}$OC=$\frac{k}{2}$��
��$\frac{\frac{k}{2}}{1}=\frac{AQ}{\frac{1}{k}}$��
��AQ=$\frac{1}{2}$��
��GO���M����
�������߳�������֪��GO=QG=1��
��AG=AQ+GO=$\frac{3}{2}$��
���ɹ��ɶ�������ã�AO=$\sqrt{��\frac{3}{2}��^{2}-{1}^{2}}$=$\frac{\sqrt{5}}{2}$��
��$\frac{1}{k}$=$\frac{\sqrt{5}}{2}$��
��k=$\frac{2\sqrt{5}}{5}$��
���� ��1�����⿼����κ������ۺ����⣬�漰���������ε��ж������ʣ�Բ�ܽǶ��������߳����������ɶ�����֪ʶ�����ݽ�Ϊ�ۺϣ�֪ʶ��϶࣬��Ҫѧ�����������ѧ֪ʶ���н��

��-1-1=0����$\frac{4^2}{5}=\frac{16}{25}$���ۣ�-1��2004=2004����-42=-16����$\frac{1}{3}-\frac{1}{2}=\frac{1}{6}$����-5��$\frac{1}{3}$��3=-5��
������ȷ����ʽ�ĸ����ǣ�������
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| ���� | ���� | ÿ������������/��Ԫ |
| A | 1 | 36 |
| B | 6 | 27 |
| C | 8 | 16 |
| D | 11 | 20 |
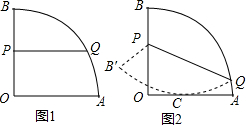 ��ͼ������OAB�İ뾶Ϊ4����AOB=90�㣬P�ǰ뾶OB��һ���㣬Q�ǻ�AB�ϵ�һ���㣮
��ͼ������OAB�İ뾶Ϊ4����AOB=90�㣬P�ǰ뾶OB��һ���㣬Q�ǻ�AB�ϵ�һ���㣮