题目内容
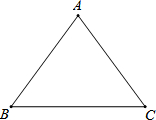 如图,在△ABC中,AB=AC,BC=32,tanC=
如图,在△ABC中,AB=AC,BC=32,tanC=| 3 |
| 2 |
考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线;运用三角函数的定义求出AE的长度;借助重心的性质求出BO、OE的长度;运用勾股定理求出BO的长度;进而求出BF的长度;借助三角函数的定义即可解决问题.
解答: 解:如图,点F为AC边的中点;连接BF;过点A作AE⊥BC;
解:如图,点F为AC边的中点;连接BF;过点A作AE⊥BC;
∵AB=AC,BC=32,
∴BE=CE=16,点O为△ABC的重心;
∵tanC=
,
∴AE=
×16=24,
∴OE=
×24=8;
由勾股定理得:BO2=BE2+OE2,
∴BO=8
,而点O为△ABC的重心,
∴BF=
×8
=12
;
由题意得:BM=
BF=6
,且DM⊥BF;
∵cos∠MBD=
=
,
∴BD=15.
故答案为15.
 解:如图,点F为AC边的中点;连接BF;过点A作AE⊥BC;
解:如图,点F为AC边的中点;连接BF;过点A作AE⊥BC;∵AB=AC,BC=32,
∴BE=CE=16,点O为△ABC的重心;
∵tanC=
| 3 |
| 2 |
∴AE=
| 3 |
| 2 |
∴OE=
| 1 |
| 3 |
由勾股定理得:BO2=BE2+OE2,
∴BO=8
| 5 |
∴BF=
| 3 |
| 2 |
| 5 |
| 5 |
由题意得:BM=
| 1 |
| 2 |
| 5 |
∵cos∠MBD=
| BE |
| BO |
| BM |
| BD |
∴BD=15.
故答案为15.
点评:该题主要考查了翻折变换的性质及其应用问题;牢固掌握等边三角形的性质、翻折变换的性质是灵活解题的基础和关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 把六张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为acm,宽为bcm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
把六张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为acm,宽为bcm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )| A、4bcm |
| B、(3a+b)cm |
| C、(2a+2b)cm |
| D、(a+3b)cm |
 图中,同旁内角的对数为( )
图中,同旁内角的对数为( )| A、14 | B、16 | C、18 | D、20 |
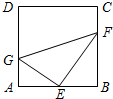 如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )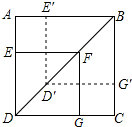 如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′.
如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′.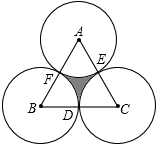 如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为
如图,正三角形ABC的边长为4,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,2为半径作圆,则图中的阴影面积为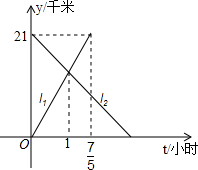 甲乙两人分别从相距21千米的A,B两地同时出发,相向而行,如图,l1,l2分别表示甲乙两人距A地的距离y(千米)与时间t(小时)之间的关系
甲乙两人分别从相距21千米的A,B两地同时出发,相向而行,如图,l1,l2分别表示甲乙两人距A地的距离y(千米)与时间t(小时)之间的关系 在如图的正方形网格图中,直线MN和线段AB上的点A、B、M、N均在小正方形的格点上,在图中:
在如图的正方形网格图中,直线MN和线段AB上的点A、B、M、N均在小正方形的格点上,在图中: