题目内容
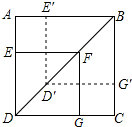 如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′.
如图,大正方形ABCD内有一个小正方形DEFG,对角线DF长为6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′.(1)求大正方形ABCD的面积;
(2)求小正方形DEFG移动到正方形D′E′BG′这个过程中扫过的面积.
考点:平移的性质
专题:
分析:(1)先求出BD的长,再根据勾股定理求出AB的长,进而可得出结论;
(2)连接EG,E′G′,EE′,GG′,根据图形平移的性质可知,小正方形DEFG移动到正方形D′E′BG′这个过程中扫过的面积即为正方形EGG′E′的面积.
(2)连接EG,E′G′,EE′,GG′,根据图形平移的性质可知,小正方形DEFG移动到正方形D′E′BG′这个过程中扫过的面积即为正方形EGG′E′的面积.
解答: 解:(1)∵DF=6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′,
解:(1)∵DF=6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′,
∴BD=6+3=9.
∵四边形ABCD是正方形,
∴2AB2=BD2,即AB2=
BD2=
×9×9=
(cm2);
(2)连接EG,E′G′,EE′,GG′,
∵四边形DEFG是正方形,
∴EG=DF=6cm,
∴S正方形EGG′E′=EG×D′F=6×3=18(cm).
 解:(1)∵DF=6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′,
解:(1)∵DF=6cm,已知小正方形DEFG向东北方向平移3cm就得到正方形D′E′BG′,∴BD=6+3=9.
∵四边形ABCD是正方形,
∴2AB2=BD2,即AB2=
| 1 |
| 2 |
| 1 |
| 2 |
| 81 |
| 2 |
(2)连接EG,E′G′,EE′,GG′,
∵四边形DEFG是正方形,
∴EG=DF=6cm,
∴S正方形EGG′E′=EG×D′F=6×3=18(cm).
点评:本题考查的是平移的性质,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
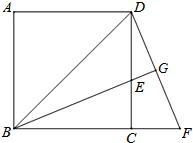 如图,四边形ABCD是正方形,点F在BC延长线上,且BF=BD,G为DF中点,BG与DC交于点E,以下结论正确的有
如图,四边形ABCD是正方形,点F在BC延长线上,且BF=BD,G为DF中点,BG与DC交于点E,以下结论正确的有①△BCE≌△DCF ②E是CD中点
③△BCE∽△DGE ④2DG2=DE•DC.
 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.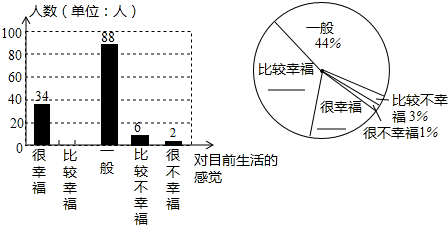
 如图,在△ABC中,AB=AC,BC=32,tanC=
如图,在△ABC中,AB=AC,BC=32,tanC= 如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F,点G,H分别为AD,BC的中点,试证明EF和GH互相平分.
如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F,点G,H分别为AD,BC的中点,试证明EF和GH互相平分.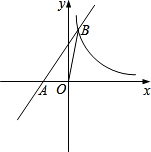 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(-1,0),与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(-1,0),与反比例函数y= 小明对自己所在班级的学生平均每周参加课外活动的时间进行了调查,由调查结果的部分数据填在了如下的表格中,并绘制了频数分布直方图,根据图表中信息回答下列问题:
小明对自己所在班级的学生平均每周参加课外活动的时间进行了调查,由调查结果的部分数据填在了如下的表格中,并绘制了频数分布直方图,根据图表中信息回答下列问题: