Question

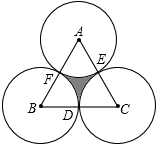如图，正三角形ABC的边长为4，D、E、F分别为BC、CA、AB的中点，以A、B、C三点为圆心，2为半径作圆，则图中的阴影面积为

 

．

Answer 1

考点：扇形面积的计算

专题：

分析：连接AD，由等边三角形的性质可知AD⊥BC，∠A=∠B=∠C=60°，根据S_阴影=S_△ABC-3S_扇形AEF即可得出结论．

解答：解：连接AD，
∵正三角形ABC的边长为4，D、E、F分别为BC、CA、AB的中点，
∴AD⊥BC，∠A=∠B=∠C=60°．
∵AB=4，
∴AD=AB•sin60°=4×

3

2

=2

3

，
∴S_阴影=S_△ABC-3S_扇形AEF=

1

2

×4×2

3

-3×

60π×22

360

=4

3

-2π．
故答案为：4

3

-2π．

点评：本题考查的是扇形的面积，熟记扇形的面积公式是解答此题的关键．