题目内容
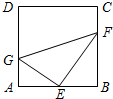 如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )
如图,在正方形ABCD中,E为AB边的中点,G,F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为( )| A、3 | B、4 | C、5 | D、6 |
考点:相似三角形的判定与性质,勾股定理
专题:
分析:证明△AGE∽△BEF,得到AE=BE=
;由勾股定理求得GE2、EF2,进而求得GF2即可解决问题.
| 2 |
解答: 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,
∴∠A=∠B=90°;而∠GEF=90°,
∴∠AGE+∠AEG=∠AEG+∠FEB,
∴∠AGE=∠FEB,
∴△AGE∽△BEF,
∴
=
,而AG=1,BF=2,AE=BE,
∴AE=BE=
;
由勾股定理得:GE2=AG2+AE2,EF2=BE2+BF2,
∴GE2=3,EF2=6,
∴GF2=GE2+EF2=9,
∴GF=3,
故选A.
 解:∵四边形ABCD为正方形,
解:∵四边形ABCD为正方形,∴∠A=∠B=90°;而∠GEF=90°,
∴∠AGE+∠AEG=∠AEG+∠FEB,
∴∠AGE=∠FEB,
∴△AGE∽△BEF,
∴
| AG |
| BE |
| AE |
| BF |
∴AE=BE=
| 2 |
由勾股定理得:GE2=AG2+AE2,EF2=BE2+BF2,
∴GE2=3,EF2=6,
∴GF2=GE2+EF2=9,
∴GF=3,
故选A.
点评:该题以正方形为载体,以考查相似三角形的判定及其性质等几何知识点为核心构造而成;灵活运用相似三角形的判定及其性质、勾股定理等知识点是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
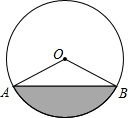 下图是输水管的切面,阴影部分是有水部分,其中水面AB宽16cm,水最深4cm.
下图是输水管的切面,阴影部分是有水部分,其中水面AB宽16cm,水最深4cm.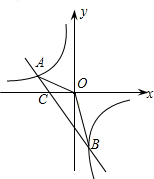 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=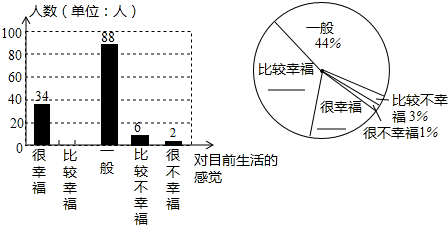
 如图,AD∥BE∥FC,它们依次交直线l1、l2于点A、B、C和点D、E、F.如果AB=2,BC=3,那么
如图,AD∥BE∥FC,它们依次交直线l1、l2于点A、B、C和点D、E、F.如果AB=2,BC=3,那么 如图,在△ABC中,AB=AC,BC=32,tanC=
如图,在△ABC中,AB=AC,BC=32,tanC= 如图,已知抛物线y=
如图,已知抛物线y= 在⊙O中,AB为⊙0的直径,AC是弦,OC=4cm∠OAC=60°,如图所示,一动点M从点A出发,在⊙O上按逆时针方向运动,当S=△MAO=S△AOC时,动点M所经过的弧长是
在⊙O中,AB为⊙0的直径,AC是弦,OC=4cm∠OAC=60°,如图所示,一动点M从点A出发,在⊙O上按逆时针方向运动,当S=△MAO=S△AOC时,动点M所经过的弧长是