题目内容
18.(1)解方程:(x-1)2=4(2)解方程:$\frac{1}{8}$x3+1=0
(3)化简:|$\sqrt{3}$-$\sqrt{2}$|+|1-$\sqrt{2}$|-|3-π|
分析 (1)方程利用平方根定义开方即可求出x的值;
(2)方程变形后,利用立方根定义开立方即可求出x的值;
(3)原式利用绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)开方得:x-1=±2,
解得:x=3或x=-1;
(2)方程变形得:x3=-8,
开立方得:x=-2;
(3)原式=$\sqrt{3}$-$\sqrt{2}$+$\sqrt{2}$-1-(π-3)=$\sqrt{3}$+2-π.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8.找出以下图形变化的规律,则第2015个图形中黑色正方形的数量是( )


| A. | 3020 | B. | 3021 | C. | 3022 | D. | 3023 |
3.货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:
(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
| 行驶时间x(时) | 0 | 1 | 2 | 3 | 4 |
| 余油量y(升) | 150 | 120 | 90 | 60 | 30 |
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
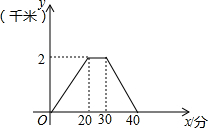 星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )
星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )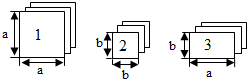 如图,有足够多的长方形和正方形卡片,
如图,有足够多的长方形和正方形卡片,