题目内容
3.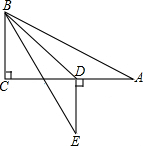 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.
分析 连接AE,先证明△ABE是顶角为30°等腰三角形,再证明△BCD是等腰直角三角形即可解决问题.
解答 解: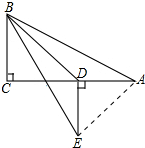 连接AE,
连接AE,
∵△BDE是由△BDA翻折,∠BAC=30°,
∴AD=DE,BA=BE,∠DBA=∠DBE,
∵AD⊥DE,
∴∠DEA=∠DAE=45°,∠BAE=∠BEA=75°,
∴∠ABE=180°-∠BAE-∠BEA=30°,
∴∠DBA=∠DBE=15°,
∴∠CDB=∠DBA+∠CAB=45°,
∵∠C=90°,
∴∠CBD=∠CDB=45°,
∴BC=CD,
在RT△BAC中,∵AB=8,∠CAB=30°,
∴BC=$\frac{1}{2}$AB=4,AC=$\sqrt{3}$BC=4$\sqrt{3}$,
∴CD=4,AD=DE-AC-CD=4$\sqrt{3}$-4.
故答案为4$\sqrt{3}$-4
点评 本题考查翻折变换、等腰直角三角形的判定和性质、直角三角形30度角的性质,发现特殊三角形是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
15.下列关于x的方程中,一定有实数根的是( )
| A. | $\sqrt{2x+3}$+4=0 | B. | $\sqrt{x-7}$+$\sqrt{x}$=7 | C. | $\sqrt{x-3}$=1-x | D. | $\sqrt{x-1}$+$\sqrt{1-x}$=3 |
13.下列实数中,是无理数的是( )
| A. | 0 | B. | $\frac{2}{7}$ | C. | 3.141414… | D. | $\sqrt{2}$ |
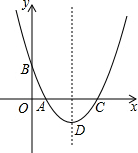 如图,已知二次函数y=x2+bx+c的图象关于直线x=2对称,且与x轴交于A、C两点,与y轴交于点B,点C与坐标原点不重合,其坐标为(c,0).
如图,已知二次函数y=x2+bx+c的图象关于直线x=2对称,且与x轴交于A、C两点,与y轴交于点B,点C与坐标原点不重合,其坐标为(c,0). 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AB=CD,请你再添加个条件,使得AE=DF,并说明理由.
如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AB=CD,请你再添加个条件,使得AE=DF,并说明理由.