题目内容
13.先化简,再求代数式$\frac{{a}^{2}-{b}^{2}}{a}÷$(a-$\frac{2ab-{b}^{2}}{a}$)的值,其中a=1+2cos45°,b=2sin30°-$\sqrt{2}$.分析 先根据分式混合运算的法则把原式进行化简,再求出a、b的值代入进行计算即可.
解答 解:原式=$\frac{(a+b)(a-b)}{a}$÷$\frac{(a-b)^{2}}{a}$
=$\frac{(a+b)(a-b)}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{a+b}{a-b}$,
当a=1+2cos45°=1+2×$\frac{\sqrt{2}}{2}$=1+$\sqrt{2}$,b=2sin30°-$\sqrt{2}$=2×$\frac{1}{2}$-$\sqrt{2}$=1-$\sqrt{2}$时,
原式=$\frac{1+\sqrt{2}+1-\sqrt{2}}{1+\sqrt{2}-1+\sqrt{2}}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
1.下面4个图案中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.如果反比例函数y=$\frac{k}{x}$的图象经过点(-2,3),那么该函数的图象也经过点( )
| A. | (-2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
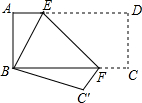 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB=55度.
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB=55度. 如图,活动课上,小王想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小王的步行速度是20米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:$\sqrt{2}$≈1.41).
如图,活动课上,小王想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小王的步行速度是20米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:$\sqrt{2}$≈1.41).
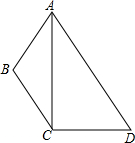 如图,在四边形ABCD中,∠D=60°,∠B是钝角,对角线AC平分∠BAD.
如图,在四边形ABCD中,∠D=60°,∠B是钝角,对角线AC平分∠BAD.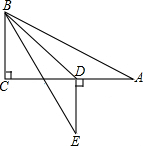 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.