题目内容
18.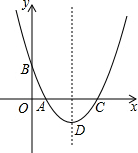 如图,已知二次函数y=x2+bx+c的图象关于直线x=2对称,且与x轴交于A、C两点,与y轴交于点B,点C与坐标原点不重合,其坐标为(c,0).
如图,已知二次函数y=x2+bx+c的图象关于直线x=2对称,且与x轴交于A、C两点,与y轴交于点B,点C与坐标原点不重合,其坐标为(c,0).(1)求出该函数的解析式,并写出其顶点D的坐标.
(2)若将此抛物线平移,使其顶点为点B,需如何平移?写出平移后抛物线的解析式.
分析 (1)利用对称轴公式求出b,再把点C(c,0)代入即可解决.
(2)根据平移的规律向左平移2的单位向上平移4个单位即可,平移前后a相同,根据顶点坐标即可写出解析式.
解答 解:(1)∵对称轴x=2=-$\frac{b}{2a}$=-$\frac{b}{2}$,
∴b=-4,
把(c,0)代入y=x2-4x+c得c2-4c+c=0,c=3(或0舍弃),
∴二次函数为y=x2-4x+3,
∵y=(x-2)2-1,
∴顶点D(2,-1).
(2)将此抛物线平移,使其顶点为点B,需要向左平移2的单位向上平移4个单位.
平移后的解析式y=x.
点评 本题考查二次函数图象的平移与几何变换,熟练掌握平移的规律是解决问题的关键,记住对称轴x=-$\frac{b}{2a}$,抛物线的顶点式y=a(x-h)2+k,顶点(h,k),属于中考常考题型

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.如果反比例函数y=$\frac{k}{x}$的图象经过点(-2,3),那么该函数的图象也经过点( )
| A. | (-2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
 如图,△ABC中,∠B=90°,BC=2AB,则cosA=$\frac{\sqrt{5}}{5}$.
如图,△ABC中,∠B=90°,BC=2AB,则cosA=$\frac{\sqrt{5}}{5}$.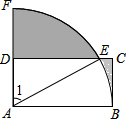 如图,在矩形ABCD中,AB=4,BC=2,以A为圆心,AB的长为半径画弧,交DC于点E,交AD延长线于点F,则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π.
如图,在矩形ABCD中,AB=4,BC=2,以A为圆心,AB的长为半径画弧,交DC于点E,交AD延长线于点F,则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π.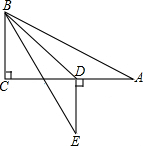 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.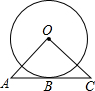 如图,AC经过⊙O上的一点B,AB=BC,连接OA、OC,∠A=∠C,求证:AB是⊙O的切线.
如图,AC经过⊙O上的一点B,AB=BC,连接OA、OC,∠A=∠C,求证:AB是⊙O的切线. 已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.
已知一次函数y=kx+b的图象与直线y=2x-$\sqrt{3}$平行,它与x轴、y轴分别相交于点A、B;它在y轴上的截距是4.平面直角坐标系的坐标原点为O.