题目内容
14.在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D,CD=$\frac{12}{5}$cm.分析 先根据勾股定理求出直角边AC的长度,再利用三角形的面积即可求出CD的长.
解答  解:∵在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,
解:∵在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4cm.
∵S△ABC=$\frac{1}{2}$AC•CB=$\frac{1}{2}$AB•CD,
∴$\frac{1}{2}$×4×3=$\frac{1}{2}$×5×CD,
∴CD=$\frac{12}{5}$cm.
故答案为$\frac{12}{5}$cm.
点评 此题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.利用直角三角形面积的两种不同表示方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.据统计,今年春节期间(除夕到初五),微信红包总收发次数达321亿次,几乎覆盖了全国75%的网民,数据“321亿”用科学记数法可表示为( )
| A. | 3.21×108 | B. | 321×108 | C. | 321×109 | D. | 3.21×1010 |
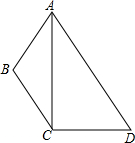 如图,在四边形ABCD中,∠D=60°,∠B是钝角,对角线AC平分∠BAD.
如图,在四边形ABCD中,∠D=60°,∠B是钝角,对角线AC平分∠BAD. 如图,△ABC中,∠B=90°,BC=2AB,则cosA=$\frac{\sqrt{5}}{5}$.
如图,△ABC中,∠B=90°,BC=2AB,则cosA=$\frac{\sqrt{5}}{5}$.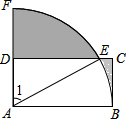 如图,在矩形ABCD中,AB=4,BC=2,以A为圆心,AB的长为半径画弧,交DC于点E,交AD延长线于点F,则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π.
如图,在矩形ABCD中,AB=4,BC=2,以A为圆心,AB的长为半径画弧,交DC于点E,交AD延长线于点F,则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π.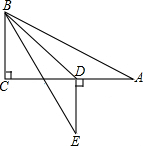 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着BD翻折后,点A落在点E处,如果AD⊥DE、那么DE的长度为4$\sqrt{3}-4$.