题目内容
10.如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.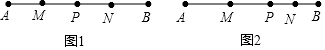
(1)如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.
分析 (1)首先根据点M是线段AP的中点,MP=4cm,求出AP的长度是多少;然后根据点P是线段AB的中点,求出线段AB的长是多少即可.
(2)根据点M是线段AP的中点,点N是线段PB的中点,可得MP=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,据此判断出MN=$\frac{1}{2}$AB,求出线段MN的长是多少即可.
解答 解:(1)∵M是线段AP的中点,MP=4cm,
∴AP=2MP=2×4=8(cm),
又∵点P是线段AB的中点,
∴AB=2AP=2×8=16(cm).
(2)∵点M是线段AP的中点,点N是线段PB的中点,
∴MP=$\frac{1}{2}$AP,PN=$\frac{1}{2}$PB,
∴MN=MP+PN=$\frac{1}{2}$AP+$\frac{1}{2}$PB=$\frac{1}{2}$(AP+PB)=$\frac{1}{2}$AB,
∵AB=12cm,
∴MN=12÷2=6(cm).
点评 此题主要考查了两点间的距离的求法,以及线段中点的性质和应用,要熟练掌握,解答此题的关键是要明确:线段的中点将线段分成长度相等的两个线段.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )| A. | -3<x<2 | B. | -3<x<0或x>2 | C. | x>-3 | D. | x<2 |
18.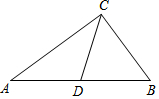 已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
 已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )
已知Rt△ABC中,∠ACB=90°,∠B=54°,CD是斜边AB上的中线,则∠ACD的度数是( )| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
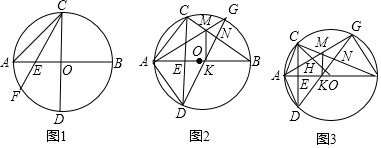
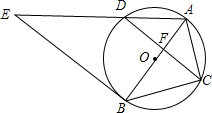 如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.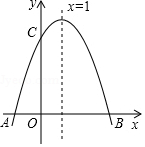 如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.
如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.